Setup and backtracking
Creation date: 2019-09-05
This is an ongoing series about: How to build a constraint solver? If you haven't read this post: Perfect as it is part 1 ;)
Otherwise have a look at the sidebar on the left for all posts in this series.
More than 2 years ago I wrote a Sudoku solver in Python. I really enjoyed it and therefore I've spend some time to do the same in Julia just faster ;) Then I wanted to build a whole constraint-programming solver in Julia. Well I actually still want to do it. It will be hard but fun. I want to share my way on my blog and instead of writing when I've done something I want to share my journey while I'm doing it.
Additionally the blog should be as simple as possible and everyone should be able to follow step by step.
In my dream we are building this together so if there is someone out there who is crazy and wants to build a constraint-programming solver from scratch... Send me a mail (o.kroeger@opensourc.es) and/or comment on this post.
Edit: Some reasons why :) If you want to know how a constraint solver works maybe it's the best idea to simply build one ;) What is a constraint solver and what does a constraint solver solve?
It's a general tool to solve problems which can be specified by constraints like
all_different,sum, ... Theall_differentconstraint for example is not part of a LP solver. In general we solve discrete problems like sudoku, graph coloring, scheduling etc.The idea is to find a feasible solution which fulfill all given constraints like in sudoku or sometimes find an optimal solution given some optimization function as in graph coloring.
Join me on the journey of how to build a constraint solver from scratch using the high level programming language julia.
In this first post I'll create the package and create test cases as well as building the most basic solver using backtracking. In the next stages we will build the alldifferent, straights, sum constraint and so on together. The next post will be similar to the previous Sudoku post but with animation and of course written in Julia.
Create a package
Before I show you the steps here you might want to check my new post on how to work with the package manager. It shows how to install, update, remove packages as well as working with environments.
First we create a package:
(v1.2) pkg> generate ConstraintSolver
Generating project ConstraintSolver:
ConstraintSolver/Project.toml
ConstraintSolver/src/ConstraintSolver.jl
(v1.2) pkg> activate ConstraintSolver/
Activating environment at `~/Julia/ConstraintSolver/Project.toml`
(v1.2) pkg> develop .
Resolving package versions...
Updating `~/.julia/environments/v1.2/Project.toml`
[e0e52ebd] + ConstraintSolver v0.1.0 [`../../../Julia/ConstraintSolver`]
Updating `~/.julia/environments/v1.2/Manifest.toml`
[e0e52ebd] + ConstraintSolver v0.1.0 [`../../../Julia/ConstraintSolver`]Info: You get to the package mode with ].
I want to have a git repository for the project and we can do this inside the julia shell as well.
shell> cd ConstraintSolver/
/Users/olek/Code/ConstraintSolver
shell> git init
Initialized empty Git repository in /Users/olek/Code/ConstraintSolver/.git/Info: You get to the shell mode with ;.
The next thing for me is always to create a simple test file which I call current.jl which is inside .gitignore so that I can test the same thing on different branches.
shell> mkdir test
shell> touch test/current.jl
shell> vim .gitignoreIn the .gitignore:
test/current.jlor maybe a whole folder
test/currentNow before we do something like loading modules I would advise to use Revise which helps in general to avoid reloading the REPL when we change code.
You might want to read my blog about Revise in my starter section.
julia> using ReviseThe current.jl file is not a real test it's more like a playground.
The basic user interface
Inside I wrote:
using ConstraintSolver
CS = ConstraintSolver
include("sudoku_fcts.jl")
function main()
com = CS.init()
grid = zeros(Int8,(9,9))
grid[1,:] = [0 0 0 5 4 6 0 0 9]
grid[2,:] = [0 2 0 0 0 0 0 0 7]
grid[3,:] = [0 0 3 9 0 0 0 0 4]
grid[4,:] = [9 0 5 0 0 0 0 7 0]
grid[5,:] = [7 0 0 0 0 0 0 2 0]
grid[6,:] = [0 0 0 0 9 3 0 0 0]
grid[7,:] = [0 5 6 0 0 8 0 0 0]
grid[8,:] = [0 1 0 0 3 9 0 0 0]
grid[9,:] = [0 0 0 0 0 0 8 0 6]
add_sudoku_constr!(com, grid)
status = CS.solve(com)
println("Status: ", status)
CS.print_search_space(com)
endFirst we load our module and then we assign it to a shorter name. We will write the constraints of the Sudoku into the file sudoku_fcts.jl and in main we first initialize a com (constraint optimization model) then we define the specific sudoku puzzle, add the constraints and solve the model. In the end we want to print the solution or the search space if it's not yet solved.
A bit about the general idea of the constraint programming solver:
We always have a search space which contains the current possible values to each index if the index isn't already solved.
Therefore we first have to create the search space which depends on the grid and on which values can be used in general (here 1-9) as well as a way to tell the solver which value in our grid corresponds to the current undefined positions (here 0).
This is my idea of the "UserInterface":
function add_sudoku_constr!(com, grid)
CS.build_search_space(com, grid, [1,2,3,4,5,6,7,8,9], 0)
for rc=1:9
#row
CS.add_constraint(com, CS.all_different, CartesianIndices((rc:rc,1:9)))
#col
CS.add_constraint(com, CS.all_different, CartesianIndices((1:9,rc:rc)))
end
for br=0:2
for bc=0:2
CS.add_constraint(com, CS.all_different, CartesianIndices((br*3+1:(br+1)*3,bc*3+1:(bc+1)*3)))
end
end
endThe first line inside the function creates the search space with the current grid, the possible values and the value we want to replace in our grid. Then for each row, each column and each block we call the all_different constraint with the corresponding indices.
If you want to know what CartesianIndices are you can for example use the help mode inside the REPL.
help?> CartesianIndicesInfo: You get to the help mode with ?.
There you'll see something like:
julia> cartesian = CartesianIndices((1:3, 1:2))
3×2 CartesianIndices{2,Tuple{UnitRange{Int64},UnitRange{Int64}}}:
CartesianIndex(1, 1) CartesianIndex(1, 2)
CartesianIndex(2, 1) CartesianIndex(2, 2)
CartesianIndex(3, 1) CartesianIndex(3, 2)If we now run include("test/current.jl) there is no error anymore and just a message that the main function is created.
Now if we run main() we obviously get an error that the init function doesn't exist.
Therefore we now write inside src/ConstraintSolver.jl.
We want to have a struct which holds all the information of the model:
module ConstraintSolver
CS = ConstraintSolver
mutable struct CoM
grid :: AbstractArray
search_space :: Dict{CartesianIndex,Dict{Int,Bool}}
constraints :: Vector{Tuple}
subscription :: Dict{CartesianIndex,Vector{Int}}
pvals :: Vector{Int}
not_val :: Int
CoM() = new()
end
end # moduleThe grid will be simply the grid we want to fill (maybe there is a more appropriate name for it). The search space will be a dictionary inside a dictionary. We want to be able to simply check whether a value is part of the possible values as well as getting all possible values and can more easily deal with problems which have numbers not starting from 1 otherwise creating an array would be also a possibility.
The constraints field contains a list of constraints such that the subscription field does not need to hold all the information several times. Now the subscription field holds all the indices of the constraints which a specific index in the grid depends on. The pval field contains all generally possible values and not_val is the value which defines whether an index is done or not. The last line in the struct specifies that we can create the object without needing to fill all the fields.
function init()
return CoM()
endHere we simply want to have access to the object.
function build_search_space(com::CS.CoM, grid::AbstractArray, pvals::Vector{Int}, if_val::Int)
com.grid = copy(grid)
com.constraints = Vector{Tuple}()
com.subscription = Dict{CartesianIndex,Vector}()
com.search_space = Dict{CartesianIndex,Dict{Int,Bool}}()
com.pvals = pvals
com.not_val = if_val
for i in keys(grid)
if grid[i] == if_val
com.search_space[i] = arr2dict(pvals)
end
com.subscription[i] = []
end
endInfo about Revise:
The thing with Revise is that we have to restart the REPL if we change the struct so if you're working with me here and do that you'll get message that Revise wasn't able to handle the changes and you need to start your session again. The first command afterwards should be: using Revise.
We copy the grid here because I don't want to overwrite the input for visualization purposes at the moment. At the bottom we fill the search space and initialize the subscription arrays.
Now we have to define the arr2dict function as we want to fill the search space with all possible values. (At the moment every value is possible as we don't have any constraints yet.)
This can be done with:
function arr2dict(arr)
d = Dict{Int,Bool}()
for v in arr
d[v] = true
end
return d
endThe next things will be to build add_constraint, all_different and solve.
In the add_constraint function we want to will the subscription field. For now we assume that every constraint function only depends on the indices it corresponds to.
"""
add_constraint(com::CS.CoM, func, indices)
Add a constraint using a function name and the indices
i.e
all_different on CartesianIndices corresponding to the grid structure
"""
function add_constraint(com::CS.CoM, func, indices)
push!(com.constraints, (func, indices))
current_constraint_number = length(com.constraints)
for i in indices
# only if index is in search space
if haskey(com.subscription, i)
push!(com.subscription[i], current_constraint_number)
end
end
endThe """ ... """ is just comments above a function which can be seen in the REPL. If you do include("test/current.jl) the module is loaded as CS so you can call:
help?> CS.add_constraint
add_constraint(com::CS.CoM, func, indices)
Add a constraint using a function name and the indices i.e all_different on CartesianIndices corresponding to the grid structureThe documentation should give information about which constraints exist and so on but for now that's it.
Having a look at the inside of the function again:
push!(com.constraints, (func, indices))
current_constraint_number = length(com.constraints)
for i in indices
# only if index is in search space
if haskey(com.subscription, i)
push!(com.subscription[i], current_constraint_number)
end
endWe give the constraint an incrementing number and push the constraint (function and indices) to the index such that we will later only need the constraint index in our subscription dictionary.
In the end every white (0) field in our Sudoku will have three constraint functions.
Next I would like to create the print_search_space function first such that we will be able to always see our state.
I think the function itself is quite boring so have a look at the repository if you want: ConstraintSolver.jl
For every constraint I'll create a file in the src folder so: src/all_different.jl contains:
function all_different(com::CS.CoM, indices)
endand the file gets included right after creating the struct.
Inside the main file (ConstrainSolver.jl) we create the function solve.
function solve(com::CS.CoM)
return :NotSolved
endInfo: It is common practice in Julia to use Symbols for things like status instead of strings.
julia> main()
Status: NotSolved
1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 5 4 6 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 9
1,2,3,4,5,6,7,8,9 2 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 7
1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 3 9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 4
9 1,2,3,4,5,6,7,8,9 5 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 7 1,2,3,4,5,6,7,8,9
7 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 2 1,2,3,4,5,6,7,8,9
1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 9 3 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9
1,2,3,4,5,6,7,8,9 5 6 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 8 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9
1,2,3,4,5,6,7,8,9 1 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 3 9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9
1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 1,2,3,4,5,6,7,8,9 8 1,2,3,4,5,6,7,8,9 6The search space is definitely quite big as we didn't remove any values from it, because or constraint function is empty and more importantly we didn't even call it yet so let's do that first and after that I will visualize the search space using the Plots library and then create a file each time and post it here instead of the command line output. ;)
In constraint programming we want to know early if the problem is feasible or infeasible so if a constraint knows that it can't be fulfilled it should scream it out. Therefore every constraint returns false if there is an issue and returns true if everything seems to be fine so far.
Now let's have a look at the new solve function:
function solve(com::CS.CoM)
if length(com.search_space) == 0
return :Solved
end
feasible = true
func_calls = 0
for constraint in com.constraints
funcname, indices = constraint
if findfirst(v->v == com.not_val, com.grid[indices]) === nothing
continue
end
feasible = funcname(com, indices)
func_calls += 1
if !feasible
break
end
end
if !feasible
return :Infeasible
end
println("#func calls: ",func_calls)
if length(com.search_space) == 0
return :Solved
end
num_open = 0
for ssi in com.search_space
num_open += length(keys(ssi.second))
end
println("Size of search space: ", num_open)
return :NotSolvedIf there is no search space we can simply return "Juhu Solved" otherwise we assume that the problem is feasible until proven otherwise.
As the first step we want to iterate once over each constraint and let it do its job. Later we might want to call the same function with the same constraint twice if the values changed but for now let's do it that way.
The all different constraint
For the all_different constraint we want to know which values are fixed in the row, column or block and which indices don't have a value yet. A function for that:
function fixed_vs_unfixed(com::CS.CoM, indices)
# get all values which are fixed
fixed_vals = []
unfixed_indices = []
for i in indices
if com.grid[i] != com.not_val
push!(fixed_vals, com.grid[i])
else
push!(unfixed_indices, i)
end
end
return fixed_vals, unfixed_indices
endNow for the all_different constraint we first of all return true in the end.
Now if one value is used more than once we can return false:
function all_different(com::CS.CoM, indices)
fixed_vals , unfixed_indices = fixed_vs_unfixed(com, indices)
fixed_vals_set = Set(fixed_vals)
# check if one value is used more than once
if length(fixed_vals_set) < length(fixed_vals)
@warn "The problem is infeasible"
return false
end
return true
endIf we now change our grid in a way that it's obviously infeasible (same number in a row, col or block) we get that the problem is infeasible.
We can add
for i in unfixed_indices
for pv in fixed_vals
if haskey(com.search_space[i], pv)
delete!(com.search_space[i], pv)
if length(com.search_space[i]) == 1
only_value = collect(keys(com.search_space[i]))[1]
if in(fixed_vals_set, only_value)
@warn "The problem is infeasible"
return false
end
com.grid[i] = only_value
delete!(com.search_space, i)
end
end
end
endto the function to simply reduce our search space.
Edit: In the first version of this post I forgot delete!(com.search_space, i) but it should be there. We fixed the value so it shouldn't be part of our search space anymore. Otherwise the check length(com.search_space) == 0 to check whether the problem is solved doesn't work.
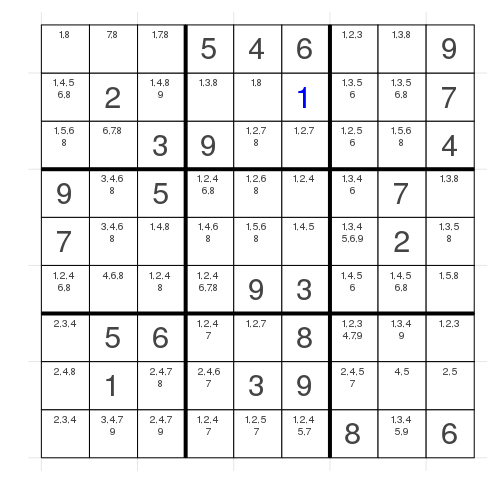
This gives us at least one new number and you might see that we could further reduce the search space because we have one new number.
We use a dictionary which holds all indices of the constraint which have changed (for now those which fix a number) and as long as something changed we will call the corresponding constraints
We add:
changed :: Dict{CartesianIndex, Bool}to the CoM struct as well as
com.changed = Dict{CartesianIndex, Bool}()in build_search_space.
Then we add this to the solve function:
while length(com.changed) > 0 && feasible
first_changed = collect(keys(com.changed))[1]
delete!(com.changed, first_changed)
constraints = com.constraints[com.subscription[first_changed]]
for constraint in constraints
funcname, indices = constraint
if findfirst(v->v == com.not_val, com.grid[indices]) === nothing
continue
end
feasible = funcname(com, indices)
func_calls += 1
if !feasible
break
end
end
endWhich basically just checks whether something changed and if that is the case then call the constraints corresponding to the entry where something changed.
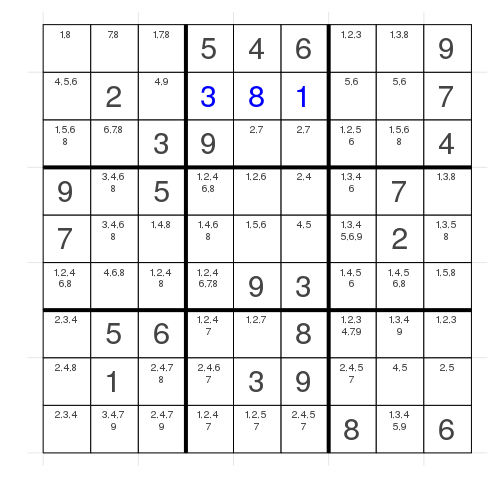
In all_different I've only added com.changed[i] = true after setting the only possible value to a grid cell.
Now let's do backtracking. We want to start at a weak point so one cell with only 2 possibilities if that is possible. Then set one and recursively try the next field. If no value is possible anymore we have to go back and try the next number or if there is none backtrack even further.
We replace the end of the solve function with:
return backtrack(com)Then we define our function to check for a weak index:
function get_weak_ind(com::CS.CoM)
lowest_num_pvals = length(com.pvals)+1
best_ind = CartesianIndex(-1,-1)
found = false
for ind in keys(com.grid)
if com.grid[ind] == com.not_val
num_pvals = length(keys(com.search_space[ind]))
if num_pvals < lowest_num_pvals
lowest_num_pvals = num_pvals
best_ind = ind
found = true
if num_pvals == 2
return found, best_ind
end
end
end
end
return found, best_ind
endIn general the idea is that we set a value into the grid even if we are not sure that the value is correct but we always keep the search_space.
Basic backtracking
Now in backtracking it is always a good idea to define when we are done at the very beginning. Here we are done if there is no weak index.
function backtrack(com::CS.CoM)
found, ind = get_weak_ind(com)
if !found
com.search_space = Dict{CartesianIndex,Dict{Int,Bool}}()
return :Solved
end
endIn that case I also empty the search space.
Further we want to iterate over all possible values and check whether the value is still possible. If there is no constraint which forbids the value we set it to the grid and call backtrack again. If the backtrack call returns :Solved we can stop as we are currently looking only for a single solution. If no value turned out to be a good choice we return :Infeasible and set our grid value back to 0.
In code this looks like this:
function backtrack(com::CS.CoM)
found, ind = get_weak_ind(com)
if !found
empty!(com.search_space)
return :Solved
end
pvals = keys(com.search_space[ind])
for pval in pvals
# check if this value is still possible
constraints = com.constraints[com.subscription[ind]]
feasible = true
for constraint in constraints
fct, indices = constraint
feasible = fct(com, indices, pval)
if !feasible
break
end
end
if !feasible
continue
end
# value is still possible => set it
com.grid[ind] = pval
status = backtrack(com)
if status == :Solved
return :Solved
end
end
com.grid[ind] = com.not_val
return :Infeasible
endWe also need to write the all_different function which takes a value and checks whether that value is allowed or whether the constraint is not satisfied anymore.
function all_different(com::CoM, indices, value::Int)
fixed_vals = [com.grid[i] for i in indices]
return !(value in fixed_vals)
endFor time measurements we can run:
using BenchmarkTools
include("test/current.jl")
@benchmark main()This measures the time after several runs and gives us some statistics:
julia> @benchmark main()
BenchmarkTools.Trial:
memory estimate: 6.54 MiB
allocs estimate: 179390
--------------
minimum time: 5.866 ms (0.00% GC)
median time: 6.625 ms (0.00% GC)
mean time: 8.178 ms (18.21% GC)
maximum time: 18.140 ms (34.91% GC)
--------------
samples: 611
evals/sample: 1We can reduce the memory a bit by rewriting the last function we wrote to this:
julia> @benchmark main()
BenchmarkTools.Trial:
memory estimate: 5.72 MiB
allocs estimate: 159842
--------------
minimum time: 5.234 ms (0.00% GC)
median time: 6.555 ms (0.00% GC)
mean time: 8.345 ms (19.31% GC)
maximum time: 31.874 ms (50.18% GC)
--------------
samples: 599
evals/sample: 1The all_different above is slow because it creates an array and the checking afterwards is another \(\mathcal{O}(n)\) so just write a loop:
for i in indices
if value == com.grid[i]
return false
end
end
return trueAnd the solved Sudoku:
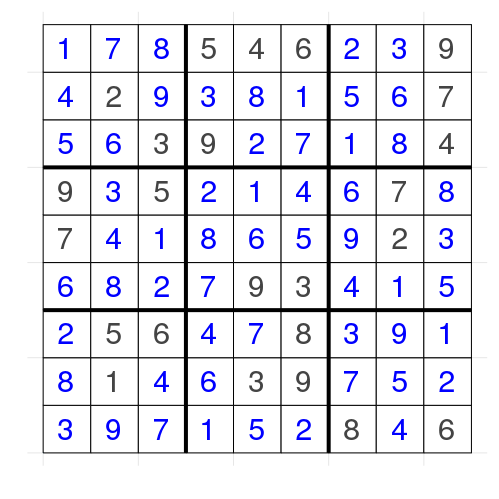
If we run this on a harder Sudoku it takes quite a bit longer. I've tested it one hard one which took 0.8s. In the next post we will reduce that to less than 10ms for the hard one.
Before writing test cases I also visualized the backtracking:
I had to add 2 additional numbers to reduce the number of steps from 3,000 to around 500.
Writing test cases
Okay now let's write test cases. :D
At the beginning we created the package and that generated a Manifest.toml and a Package.toml. We don't want to have the first in the git repo so I put it into .gitignore. Let's have a look at the Project.toml.
name = "ConstraintSolver"
uuid = "e0e52ebd-5523-408d-9ca3-7641f1cd1405"
authors = ["Ole Kröger <o.kroeger@opensourc.es>"]
version = "0.1.0"Your authors might be empty (not actually when I added it to Julia...).
The package gets a unique id and a version number. Now if the package depends on other packages which will be the case in the next steps they will be listed here as well. For testing we need the Test package.
(v1.2) pkg> activate .
Activating environment at `~/Julia/ConstraintSolver/Project.toml`
(ConstraintSolver) pkg> add TestThis will add
[deps]
Test = "8dfed614-e22c-5e08-85e1-65c5234f0b40"but actually we need it only for testing so we change it to:
[extras]
Test = "8dfed614-e22c-5e08-85e1-65c5234f0b40"
[targets]
test = ["Test"]Now we need to create the file test/runtests.jl:
using Test
using ConstraintSolver
CS = ConstraintSolver
include("sudoku_fcts.jl")
include("sudoku_tests.jl")and the test/sudoku_tests.jl file as well:
@testset "Sudoku" begin
@testset "Sudoku from opensourc.es" begin
com = CS.init()
grid = zeros(Int8, (9,9))
grid[1,:] = [0,2,1,0,7,9,0,8,5]
grid[2,:] = [0,4,5,3,1,0,0,0,9]
grid[3,:] = [0,7,0,0,4,0,0,1,0]
grid[4,:] = [0,0,0,1,0,8,0,3,6]
grid[5,:] = [0,6,0,0,0,0,2,0,8]
grid[6,:] = [0,0,0,0,0,3,0,0,4]
grid[7,:] = [6,0,8,0,0,0,0,0,0]
grid[8,:] = [0,9,4,0,0,7,8,0,0]
grid[9,:] = [2,0,0,5,0,0,0,4,0]
add_sudoku_constr!(com, grid)
@test CS.solve(com) == :Solved
@test fulfills_sudoku_constr(com)
end
endThat looks pretty similar to our current.jl file but we have @testsets and @test macros.
Okay last step is to write the fulfills_sudoku_constr.jl function:
function fulfills_sudoku_constr(com)
correct = true
for rc=1:9
vals = unique(com.grid[CartesianIndices((rc:rc,1:9))])
correct = length(vals) != 9 ? false : correct
vals = unique(com.grid[CartesianIndices((1:9,rc:rc))])
correct = length(vals) != 9 ? false : correct
end
for br=0:2
for bc=0:2
vals = unique(com.grid[CartesianIndices((br*3+1:(br+1)*3,bc*3+1:(bc+1)*3))])
correct = length(vals) != 9 ? false : correct
end
end
return correct
endI've added two other Sudokus so that my output will look a bit different (6 tests instead of 2):
(ConstraintSolver) pkg> activate
Activating environment at `~/.julia/environments/v1.2/Project.toml`
(v1.2) pkg> test ConstraintSolver
Testing ConstraintSolver
Resolving package versions...
Status `/tmp/jl_atKR7G/Manifest.toml`
[e0e52ebd] ConstraintSolver v0.1.0 [`~/Julia/ConstraintSolver`]
[2a0f44e3] Base64 [`@stdlib/Base64`]
[8ba89e20] Distributed [`@stdlib/Distributed`]
[b77e0a4c] InteractiveUtils [`@stdlib/InteractiveUtils`]
[56ddb016] Logging [`@stdlib/Logging`]
[d6f4376e] Markdown [`@stdlib/Markdown`]
[9a3f8284] Random [`@stdlib/Random`]
[9e88b42a] Serialization [`@stdlib/Serialization`]
[6462fe0b] Sockets [`@stdlib/Sockets`]
[8dfed614] Test [`@stdlib/Test`]
Test Summary: | Pass Total
Sudoku | 6 6
Testing ConstraintSolver tests passedWe also want that these tests are run in the cloud on different versions of Julia and whenever someone creates a PR on GitHub.com.
Therefore we create a .travis.yml file:
language: julia
os:
- linux
- osx
julia:
- 1.0
- 1.2
- nightly
matrix:
allow_failures:
- julia: nightly
codecov: true
cache:
directories:
- /home/travis/.juliaWe let it run on Julia 1.0 (Long term support version), the current latest release 1.2 and the latest not released build of Julia (nightly) on both linux and osx. It's okay if it fails on nightly. Additionally we want to see whether we test every part of our code with codecov.
After pushing the repository to GitHub we can set up travis-ci. There we need to activate our repository in the settings tab and then trigger the build. The codecov is shown on codecov.io.
There we see that we didn't test for any kind of infeasibility calls and the biggest blog is that we never printed the search space. I'll add that but the blog post is long enough ;)
And new posts are online:
and several more ... see the full list in the sidebar on the left.
Thanks for reading!
I'll keep you updated if there are any news on this on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de
If you enjoy the blog in general please consider a donation via Patreon. You can read my posts earlier than everyone else and keep this blog running.
Want to be updated? Consider subscribing on Patreon for free


