Constraint Solver Part 6: Backtrack and Sum constraint
Creation date: 2019-09-21
Series: Constraint Solver in Julia
This is part 6 of the series about: How to build a Constraint Programming solver?
We talked a while about one special constraint type: alldifferent and there especially about sudokus.
Let's get into the next constraint type in this blog and also a small change in backtracking.
Backtracking
First about backtracking. At the moment we use recursion and it's kind of the obvious choice for it but it has its limitations regarding recursion limit and I normally don't find it easy to debug.
The first part of this post is how to change it in a way that we don't use recursion anymore.
There are some ways of doing this:
Building an actual tree structure
Building a queue which shows the leaf nodes of a tree
Basically do the same as recursion but without it
The first one has the obvious disadvantage that we have to save everything but it's easy to do everything for example not only Depth-First-Search (DFS).
I use the second option in Juniper.jl as we normally use Best-First-Search (BFS) there and we don't need to store the tree structure. In that case the information of each node is quite small. Only the bounds of each variable so we split a node into two branches like x <= 2 and x > 2. There is no constraint propagation in the sense as we have it here.
In this project we would basically need to save the whole search space for each node which is too much I think.
Therefore I choose option 3. This limits us to DFS which is fine as long as we only deal with satisfiable problems I think.
Okay so how do we do it?
I created a backtrack object which defines what we have done in that particular node or to be more precise any information we need to remove if we need to backtrack:
mutable struct BacktrackObj
variable_idx :: Int
pval_idx :: Int
pvals :: Vector{Int}
constraint_idx :: Vector{Int}
pruned :: Vector{Vector{Int}}
BacktrackObj() = new()
endWe want to know which variable we fixed, which possible values this variable had when we started and in which iteration we are in that process. Additionally if we pruned some values we want to know which constraint was involved because we need the indices and then how many values we pruned.
Remember: pruned in ConstraintOutput is just a vector of numbers which show how many values we removed from a variable.
If we call backtrack! we have:
pvals = values(com.search_space[ind])
backtrack_obj = BacktrackObj()
backtrack_obj.variable_idx = ind
backtrack_obj.pval_idx = 0
backtrack_obj.pvals = pvals
backtrack_vec = BacktrackObj[backtrack_obj]so simple fill the object and at the moment we didn't prune anything so we leave constraint_idx and pruned empty.
while length(backtrack_vec) > 0
backtrack_obj = backtrack_vec[end]
backtrack_obj.pval_idx += 1
ind = backtrack_obj.variable_idxWe've set pval_idx to 0 before so we increase it by one here and we will use ind to refer to the index of the variable as we did before. Now there might be something we pruned before and need to revert now (not in the first call of the while loop)
if isdefined(backtrack_obj, :pruned)
reverse_pruning!(com, backtrack_obj)
endNow we check whether we tested all possible values already:
# checked every value => remove from backtrack
if backtrack_obj.pval_idx > length(backtrack_obj.pvals)
com.search_space[ind].last_ptr = length(backtrack_obj.pvals)
com.search_space[ind].first_ptr = 1
pop!(backtrack_vec)
continue
end
pval = backtrack_obj.pvals[backtrack_obj.pval_idx]That means that we need to also reset our last_ptr and first_ptr for that variable back to what it was before and remove the backtrack object from our list.
At the end of our while loop we had:
status = rec_backtrack!(com)
if status == :Solved
return :Solved
else
# we changed the search space and fixed values but didn't turn out well
# -> move back to the previous state
reverse_pruning!(com, constraints, constraint_outputs)
endSo we called the function again got something back and if we solved the problem we can return and otherwise we need to reverse prune.
Now we reverse prune at the very beginning but we need to initiate a new function call kind of (without actually calling the function):
found, ind = get_weak_ind(com)
if !found
return :Solved
end
com.info.backtrack_counter += 1
backtrack_obj.constraint_idx = zeros(Int, length(constraint_outputs))
backtrack_obj.pruned = Vector{Vector{Int}}(undef, length(constraint_outputs))
for cidx = 1:length(constraint_outputs)
constraint = constraints[cidx]
constraint_output = constraint_outputs[cidx]
backtrack_obj.constraint_idx[cidx] = constraint.idx
backtrack_obj.pruned[cidx] = constraint_outputs[cidx].pruned
end
pvals = values(com.search_space[ind])
backtrack_obj = BacktrackObj()
backtrack_obj.variable_idx = ind
backtrack_obj.pval_idx = 0
backtrack_obj.pvals = pvals
push!(backtrack_vec, backtrack_obj)We simply get our next index and then we fill our new object as I didn't want to save the complete ConstraintOutput in each node only the stuff we actually need to backtrack. This gets saved in the current backtrack object.
At the end we create and push our new backtrack object which uses the new ind we got from get_weak_ind.
After the while loop we had:
com.search_space[ind].last_ptr = previous_last_ptr
com.search_space[ind].first_ptr = 1
return :Infeasiblenow we only need:
return :InfeasibleAs we use a backtrack object now we need a new reverse_pruning function.
function reverse_pruning!(com::CS.CoM, backtrack_obj::CS.BacktrackObj)
for (i,constraint_idx) in enumerate(backtrack_obj.constraint_idx)
constraint = com.constraints[constraint_idx]
for (j,local_ind) in enumerate(constraint.indices)
com.search_space[local_ind].last_ptr += backtrack_obj.pruned[i][j]
end
end
empty!(backtrack_obj.constraint_idx)
empty!(backtrack_obj.pruned)
endWe have two reverse_pruning! functions as we still use the old one if we find out during our pruning process that it's not feasible anymore.
That's basically it for backtracking. There is no real change in performance. I've checked. It's maybe a small bit faster than before.
Sum constraint
Now to the sum constraint. It's always nice to solve a puzzle with a new constraint as it's otherwise quite boring I think. Let's not get too far away from sudoku:
We tackle Killer sudoku.
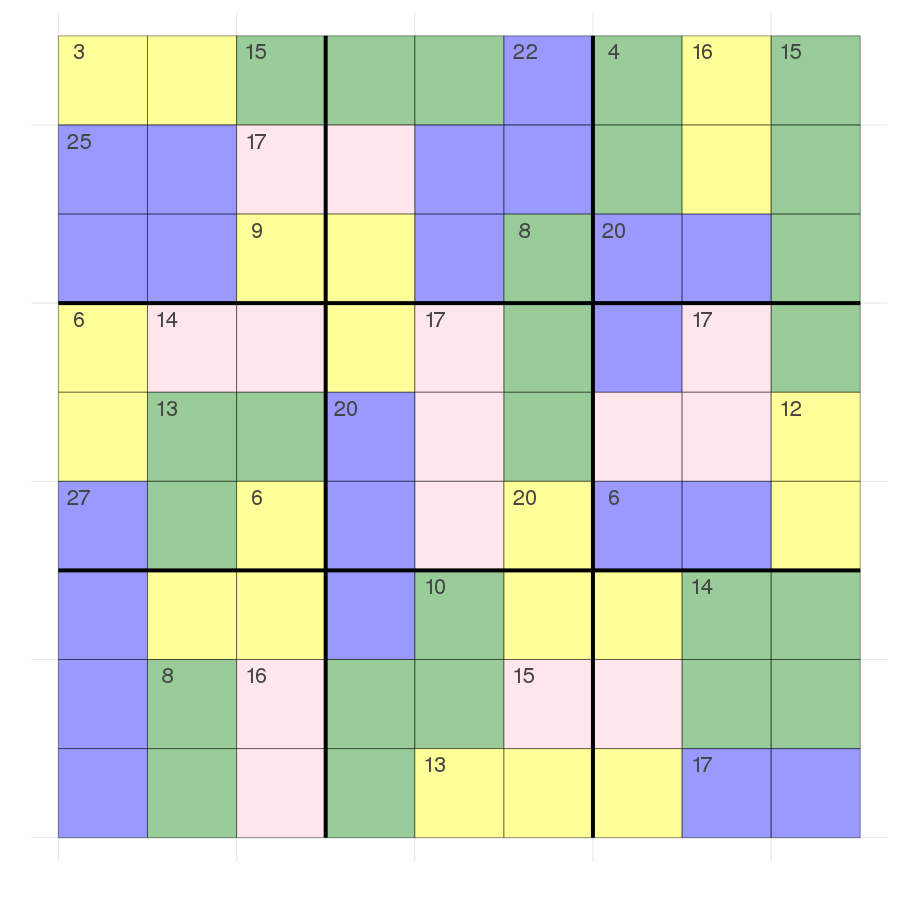
That is the killer sudoku shown on the Wikipedia page.
It is a 9x9 grid as well which itself consists of 9 3x3 grids. The rules are the same as sudoku plus one extra rule.
There are extra regions here marked in color which have a number in the upper left corner of that region.
Edit 02.10.2019: The region is called cage and I just found out that each cage has a all different constraint as well. I don't use that here as I didn't read it :/ but it's also reasonable for the solver and this and the following post, that we concentrate on the sum constraint.
This number shows the sum in that region i.e in the upper left of the grid there is a 3 so that the sum of those two yellow cells must be 3. Therefore it can be either 1,2 or 2,1. This for example fixes the number in the second row and 7th colum (below the 4) to a 3 as in that region the numbers can be only 1,3 or 3,1 as we also have the alldifferent constraint from sudoku and the first row already has a 1.
Okay rules are done.
I define the regions like this:
sums = [
(result = 3, indices = [(1, 1), (1, 2)]),
(result = 15, indices = [(1, 3), (1, 4), (1, 5)]),
(result = 22, indices = [(1, 6), (2, 5), (2, 6), (3, 5)]),
(result = 4, indices = [(1, 7), (2, 7)]),
(result = 16, indices = [(1, 8), (2, 8)]),
(result = 15, indices = [(1, 9), (2, 9), (3, 9), (4, 9)]),
...
]and then:
for s in sums
CS.add_constraint!(com, CS.eq_sum, [com_grid[CartesianIndex(ind)] for ind in s.indices]; rhs=s.result)
endSo we now have a right hand side (rhs) in our add_constraint! function and we need of course a rhs in our Constraint struct.
mutable struct Constraint
idx :: Int
fct :: Function
indices :: Vector{Int}
pvals :: Vector{Int}
rhs :: Int
endwe create a eq_sum.jl file and include it.
include("eq_sum.jl")and in add_constraint! we have:
constraint = Constraint(current_constraint_number, fct, indices, Int[], rhs)and rhs=0 as the default for our function.
I hope you remember that we have two all_different functions. One is used to check whether setting a value inside backtracking is feasible and the other main one tries to prune values.
In the former one we also need the index for where we want to set the value in eq_sum and it kind of makes sense anyway so I changed:
function all_different(com::CoM, indices, value::Int)
return !any(v->issetto(v,value), com.search_space[indices])
endto:
function all_different(com::CoM, constraint::Constraint, value::Int, index::Int)
indices = filter(i->i!=index, constraint.indices)
return !any(v->issetto(v,value), com.search_space[indices])
endNow the function itself gets all indices as it gets the constraint now and also the index where the value is set.
The first thing I want to do is to define an empty eq_sum prune function which doesn't prune anything and always returns it's feasible.
function eq_sum(com::CS.CoM, constraint::Constraint; logs = true)
changed = Dict{Int, Bool}()
pruned = zeros(Int, length(indices))
return ConstraintOutput(true, changed, pruned)which means I want to work completely with backtracking here.
Now lets check for feasibility in our second function:
function eq_sum(com::CoM, constraint::Constraint, val::Int, index::Int)
indices = filter(i->i!=index, constraint.indices)
search_space = com.search_space
csum = 0
num_not_fixed = 0
max_extra = 0
min_extra = 0
for idx in indices
if isfixed(search_space[idx])
csum += value(search_space[idx])
else
num_not_fixed += 1
max_extra += search_space[idx].max
min_extra += search_space[idx].min
end
end
if num_not_fixed == 0 && csum + val != constraint.rhs
return false
end
return trueWe check the current sum csum and then compute the maximum value we can get by all the empty cells as well as the minimum value.
At the beginning we check only if every number is fixed and if yes we add val to the current sum and check if it matches the rhs.
Before we use max_extra and min_extra let us define .max and .min of a variable first.
We can compute it every time using maximum and minimum but I think it's valuable to save it in our Variable and keep track of it there but I'm not completely sure as we don't need .min and .max for all_different so why should we compute it there? Maybe we can compute it only for variables which are part of a sum constraint or something later. For now I decided to save it in Variable and compute it when it changes.
The rm! function changes to:
function rm!(v::CS.Variable, x::Int; set_min_max=true)
ind = v.indices[x+v.offset]
v.indices[x+v.offset], v.indices[v.values[v.last_ptr]+v.offset] = v.indices[v.values[v.last_ptr]+v.offset], v.indices[x+v.offset]
v.values[ind], v.values[v.last_ptr] = v.values[v.last_ptr], v.values[ind]
v.last_ptr -= 1
if set_min_max
vals = values(v)
if length(vals) > 0
if x == v.min
v.min = minimum(vals)
end
if x == v.max
v.max = maximum(vals)
end
end
end
endHere it's a parameter to compute it or not as I add a function for remove_below and remove_above later which can compute it in the end once.
In fix! we add: v.min = x; v.max = x and that's it.
Well we actually also need to reset it reverse_pruning! which gets a new function for reverse prune a single variable which we call in our normal reverse_pruning! functions.
function single_reverse_pruning!(search_space, index::Int, prune_int::Int)
if prune_int > 0
var = search_space[index]
l_ptr = max(1,var.last_ptr)
new_l_ptr = var.last_ptr + prune_int
@views min_val = minimum(var.values[l_ptr:new_l_ptr])
@views max_val = maximum(var.values[l_ptr:new_l_ptr])
if min_val < var.min
var.min = min_val
end
if max_val > var.max
var.max = max_val
end
var.last_ptr = new_l_ptr
end
endnow back to our feasibility eq_sum function:
We can add:
if csum + val + min_extra > constraint.rhs
return false
end
if csum + val + max_extra < constraint.rhs
return false
endWhich means if we add our new value val to the current sum csum ,and then we need to add at least min_extra later, the sum is bigger than our rhs => It's not feasible the same is true if we add max_extra and it's still too low.
If we now run solve! we have to wait for a long time. (Actually I always killed it after 1 or 2 minutes I think).
So simple backtracking isn't enough.
To the prune function of eq_sum:
First we will get a list of minimum and maximum values
# compute max and min values for each index
maxs = zeros(Int, length(indices))
mins = zeros(Int, length(indices))
pre_maxs = zeros(Int, length(indices))
pre_mins = zeros(Int, length(indices))
for (i,idx) in enumerate(indices)
max_val = search_space[idx].max
min_val = search_space[idx].min
maxs[i] = max_val
mins[i] = min_val
pre_maxs[i] = max_val
pre_mins[i] = min_val
endand we have this values twice as we will change maxs and mins and want to compare later whether we changed something.
Let's have a look at a small example to explain the next step:
[0 5] + [3 4] + [1 2] == 7The structure is [min_val max_val] so we have 3 variables with different ranges and they should add up to 7.
For each variable we will do the following:
move the rhs to the left
move the current variable to the right
[3 4] + [1 2] - 7 == -[0 5]Now we can simplify the left hand side as
[4 6] - 7 == -[0 5]
-[1 3] == -[0 5]Now the left hand side is a smaller range than the right hand side so we can update the right hand side.
The simplify thing needs to be only once where we compute the total maximum over all variables (minus the right hand side) and then we can just subtract the maximum of the current variable to get the same result.
In the above case we would compute
full_max = 5+4+2 - 7and then subtract 5 from it to get the -1 we had before.
I wrote that down like this:
# for each index compute the maximum and minimum value possible
# to fulfill the constraint
full_max = sum(maxs)-constraint.rhs
full_min = sum(mins)-constraint.rhs
for (i,idx) in enumerate(indices)
if isfixed(search_space[idx])
continue
end
# minimum without current index
c_min = full_min-mins[i]
# if the minimum is already too big
if c_min > -mins[i]
return ConstraintOutput(false, changed, pruned)
end
# maximum without current index
c_max = full_max-maxs[i]
# if the maximum is already too small
if c_max < -maxs[i]
return ConstraintOutput(false, changed, pruned)
end
if c_min < -mins[i]
mins[i] = -c_min
end
if c_max > -maxs[i]
maxs[i] = -c_max
end
endand then I do the update step where I check what changed and then remove the values from the search space and set pruned and changed accordingly:
# update all
for (i,idx) in enumerate(indices)
if maxs[i] < pre_maxs[i]
nremoved = remove_below(search_space[idx], maxs[i])
if nremoved > 0
changed[idx] = true
pruned[i] += nremoved
if !feasible(search_space[idx])
return ConstraintOutput(false, changed, pruned)
end
end
end
if mins[i] > pre_mins[i]
nremoved = remove_above(search_space[idx], mins[i])
if nremoved > 0
changed[idx] = true
pruned[i] += nremoved
if !feasible(search_space[idx])
return ConstraintOutput(false, changed, pruned)
end
end
end
endEdit: I found that this is not very good explained and also not implemented as I imagined it in my brain :/ I'm sorry about that. Unfortunately it happens when blogging while coding. There is an update to that part in Part 8: UI refactoring and bugfix of sum constraint
And defined remove_below ,remove_above and feasible:
function remove_below(var::CS.Variable, val::Int)
vals = values(var)
nremoved = 0
for v in vals
if v < val
rm!(var, v; set_min_max = false)
nremoved += 1
end
end
if nremoved > 0 && feasible(var)
var.min = minimum(values(var))
end
return nremoved
end(remove_above is quite similar)
Here I only compute var.min as var.max didn't change. It might be the case that we remove everything such that no value is possible. Then we want to return ConstraintOutput(false, changed, pruned).
The feasible function is simple:
function feasible(var::CS.Variable)
return var.last_ptr >= var.first_ptr
endLet's have a look at the performance:
julia> @benchmark main(;benchmark=true)
BenchmarkTools.Trial:
memory estimate: 9.20 MiB
allocs estimate: 68067
--------------
minimum time: 5.288 ms (0.00% GC)
median time: 7.198 ms (0.00% GC)
mean time: 7.481 ms (15.48% GC)
maximum time: 80.125 ms (86.67% GC)
--------------
samples: 668
evals/sample: 1This includes creating the model and I would say that it doesn't look too bad.
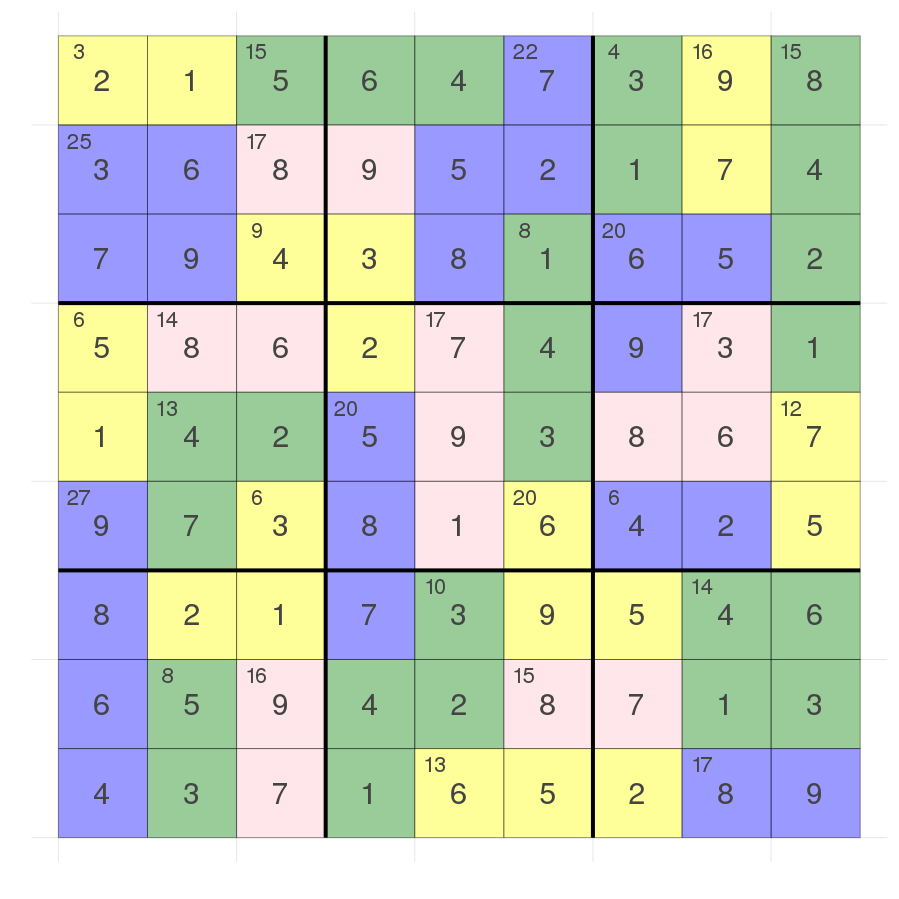
Btw this is the solved killer sudoku
Now there should be some kind of benchmarking:
Unfortunately I wasn't able to find a list of killer sudokus which I could use. For now I converted the image of some website of a killer sudoku into my data structure and that is quite cumbersome but I looked for a hard killer sudoku (whatever that actually means as I never did them myself)
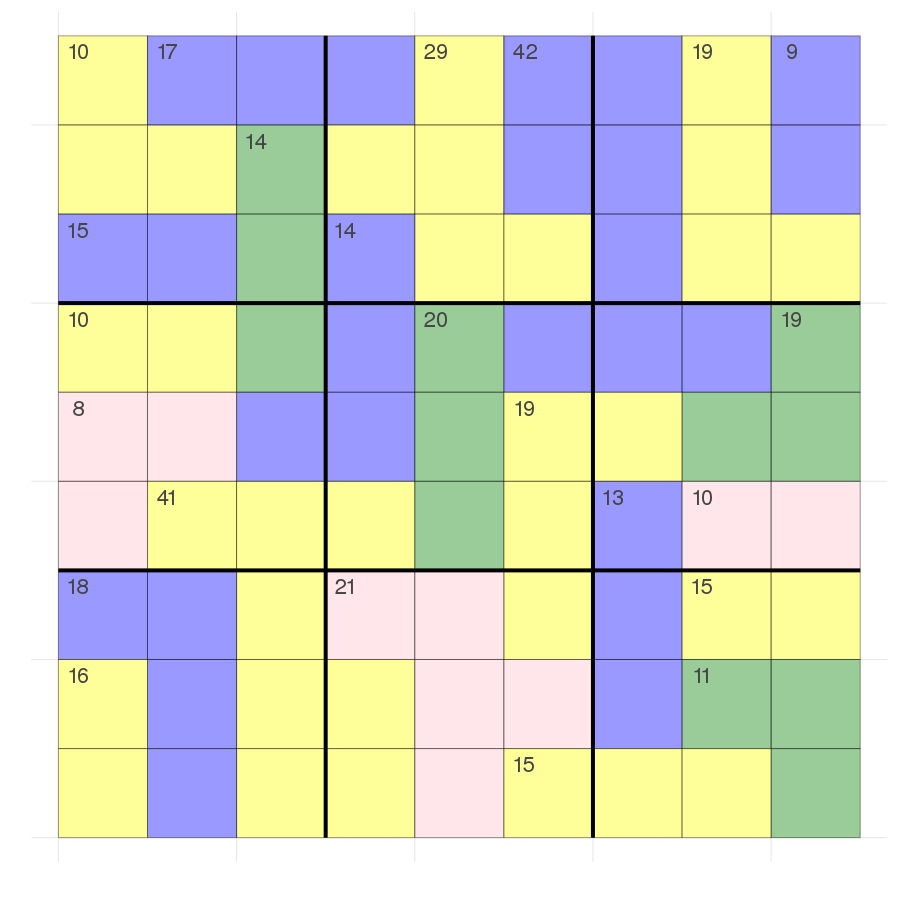
I would say there are fewer regions so that makes it harder at first glance. Let's try:
..........
ah okay waiting .....
Oh man that takes a while ...
It took more than 30s on my machine which is too long in my opinion.
The info says:
Info:
pre_backtrack_calls = 77
backtracked = true
backtrack_counter = 86647
in_backtrack_calls = 4064935Which is huge! Over 4 million function calls inside backtracking. That's just too much.
I of course forgot:
com.bt_infeasible[idx] += 1whenever it's infeasible but that doesn't change much.
What's next?
Let's have a look at how to make it faster in the next post but give an outlook here:
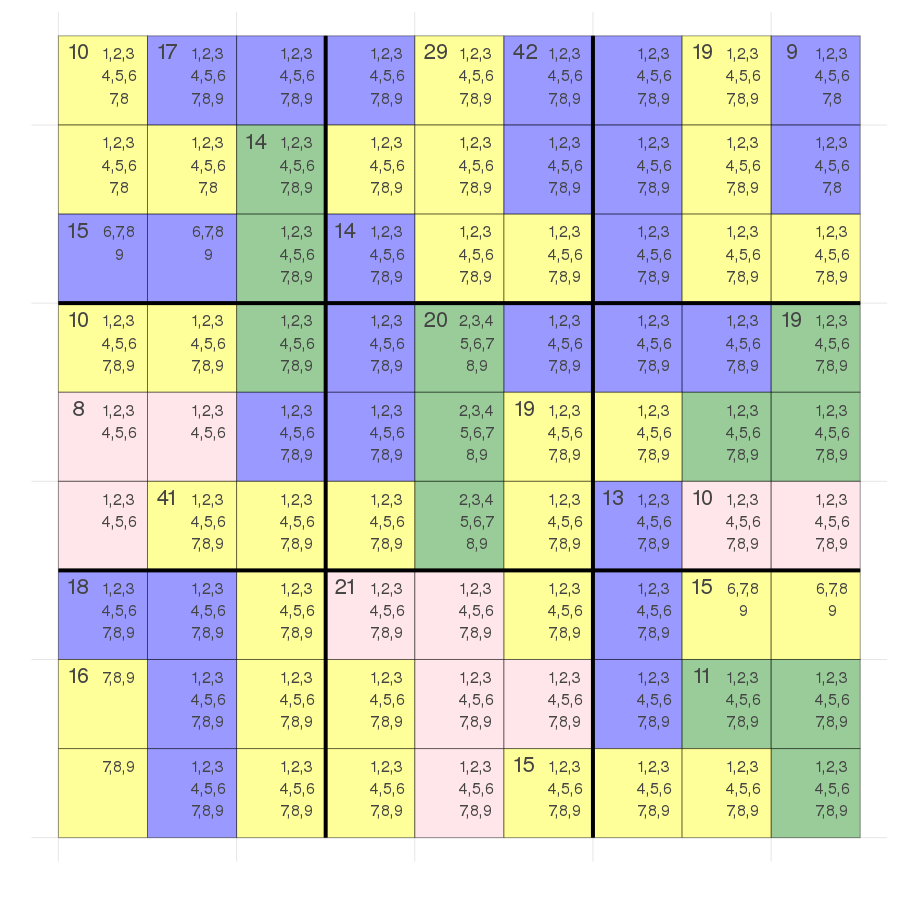
The problem I see is visible in the bottom left yellow region. There is no way to have an 8 there but the sum constraint doesn't know that as it has no idea of the all_different constraint.
In general the maximum and minimum we assume can't be achieved as we most often have the all different constraint i.e in the pink region in the fourth block (with the sum=8) it's not possible to have a 6 there as this would mean the other two cells needed to be a 1 which isn't allowed.
That means we have to link these constraints together. We'll need some kind of a lookup to check which indices share another constraint to prune more values.
Another thing is that if we have a lot of cells in a sum constraint a lot of things are possible so we should try to reduce the number of cells in a sum constraint. For example the solver should be able to deduce that we have an alldifferent constraint with 1-9 for 9 cells so every digit has to be there exactly once which means we have a sum constraint of 45. If we now look at the bottom right 3x3 box we have 4 sum constraints which add up to \(13+15+11+15 = 54\) which means that the blue cell outside + the yellow cell outside need to add up to 9. That means we would be at least be able to remove the 9 in both of them.
A lot to think about... and we don't want to make it special to killer sudoku of course. Give me some time and maybe send me ideas ;)
Same as last time:
Should the variable check whether it's feasible to set it? So whenever a variable is fixed it might should call fulfills_constraints itself and return whether it's successful as I think the person who implements constraints shouldn't handle that this directly.
Stay tuned ;)
And as always:
Thanks for reading and special thanks to my first two patrons!
Check out my update:
If you want to have early access to the next posts as well and enjoy the blog in general please consider a donation via Patreon to keep this project running.
If you have any questions, comments or improvements on the way I code or write please comment here and or write me a mail o.kroeger@opensourc.es and for code feel free to open a PR on GitHub ConstraintSolver.jl
Additionally if you want to practice code reviews or something like that I would be more than happy to send you what I have before I publish. ;)
I'll keep you updated if there are any news on this on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de
Want to be updated? Consider subscribing on Patreon for free


