Constraint Solver Part 5: Different data structure

Series: Constraint Solver in Julia

• Part One: Setup and backtracking

• Part Two: Pruning

• Part Three: Pruning+Benchmarking

• Part Four: Alldifferent constraint

This is part 5 of the series about: How to build a Constraint Programming solver?

Let's do a small recap of what we have done so far. We've created a julia package in the first post and implemented the most basic backtracking for solving a sudoku puzzle. We understood that this is pretty slow as we could use the information after we fixed a cell to a value to find out the values of cells which are connected by a constraint to that cell. In part 3 I described that these new fixes itself can be used further on which gave us a performance improvement again.

In the last post we tried not to make backtracking faster but instead tried to avoid it as much as possible by solving the sudoku in a more human like fashion.

We could now further try to reduce the number of steps we call the now slower alldifferent constraint or make it faster or change the ordering of the calls or fix values in a different ordering, as at the moment we only decide which cell we want to tackle next in backtracking but not on the ordering of how we fix the number in a cell i.e if it has the possible values 5,6,7 it might be reasonable to start with the 7 if we think that it's more likely based on some heuristics.

What I want to do instead in this post is changing the data structure a bit. We are currently working on a grid which seems to be a good choice for a sudoku and the 8-queen problem as well as magic squares but it's not always the case for example it's stupid for graph coloring so maybe we should just have linear indices internally instead of cartesian indices. Another point is that we are working with a dictionary to represent the values in our search space for each cell but adding and removing to a dictionary sometimes seems quite stupid as we set a cell in backtracking and then reset it and have to fill all the values again it had before. Maybe there is a better data structure. Besides that it seems to be reasonable to have a struct for a variable which can hold some information of that variable maybe something like a name for a country in graph coloring?

Additionally I think it's quite weird to have a grid and a search space separately if I think about it. The variable could hold the information about being fixed or not.

I found a new idea at MiniCP Part 2 (unfortunately all sites of the website have the same url :/). MiniCP is a constraint solver used in teaching constraint solving so you might in general be interested at that. Pascal Van Hentenryck who also is the professor of the online about Discrete optimization at coursera which I did three years ago works on that. Definitely check out his course!

Back to the idea: Instead of having a dictionary we hold the possibilities in a vector.

[1,2,3,4,5,6,7,8,9] now removing from a vector is much slower than from a dictionary so we have to think about that. In the reverse pruning part we would also add values back to the vector which I think is a bit stupid in the dictionary version as we kind of removing some values all the time and then want to add them again if we made a mistake.

Instead we could use a pointer which tells us how many values are still possible i.e at the beginning we say we have 9 possible values and if we remove the 9 we would have

[1,2,3,4,5,6,7,8,9], 8 where the 8 indicates that we only have 8 possible values.

Okay sure super easy if we always remove the 9 first and then 8 and then 7 and so on.

Obviously it's not so easy if we want to remove the 3 now.

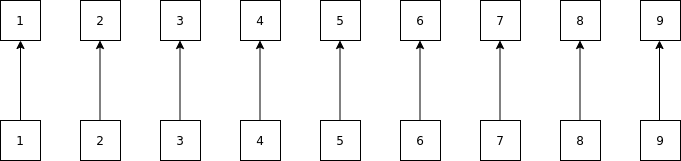
Let's start with our 9 values again and we have two vectors now. The values (values) shown in the first row and the indices (idxs) shown in the second row.

If we want to know at which position the value 7 is, we would call idxs[7] and we would get 7 back as the value 7 is at position 7 in values.

What happens now if we want to remove the 3?

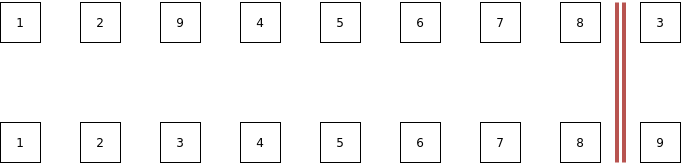
We have the red barrier which tells us that only the left part is still possible and we swapped the value which was behind that barrier but is still possible 9 with the value we want to remove 3.

Now we need to figure out the changes in the indices such that we still know where the value 3 is as we later want to have an easy check whether it's still possible or not.

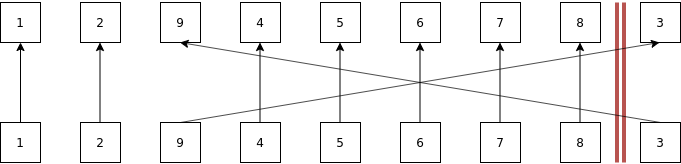
So if we want to check whether the 3 is a possible value we would do idxs[3] get 9 back and would check whether 9 is behind that barrier and see: 3 is not a possible value.

Pretty simple, right? Let's remove value 5:

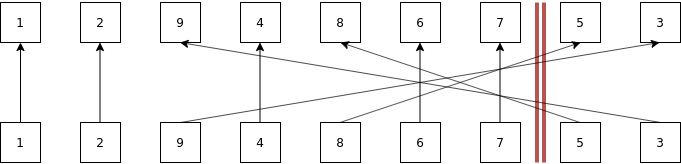
Straightforward I would assume. It gets a bit more tricky when we want to remove a value which isn't as it's initial position anymore i.e 9.

If we remove 9:

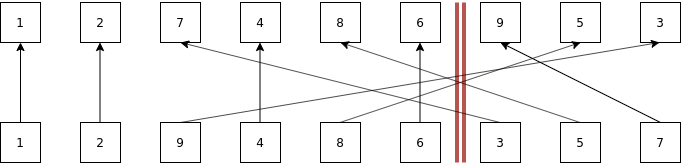
Before this the values looked exactly the same as the idxs but here that wouldn't work anymore but besides that we did what we did before as well.

We moved the red barrier then set the value which we want to remove behind that barrier and by move I mean swap its position such that we still have the values 1-9.

Therefore we had to look at which position the 9 is which was at position 3 and change the idxs vector in such a way that at the position where we now have the 9 (position 7) points to the position where the 9 was as we swapped the values.

Setting the variable to a value can be done in a similar fashion by moving the barrier to directly behind the first value and then swapping the desired value to the front.

This is what they do with MiniCP and I have a little problem with that as in backtracking we set a value and later set it to something else which is not easy using this method as we move the barrier more than one step.

My approach instead is to have two barriers one from left and one from the right. This might be a stupid idea and I see myself hating it in the future but at the moment it seems interesting so I'm sorry I do it my way...

We create a struct for our Variable in src/Variable.jl

mutable struct Variable
    idx         :: Int
    first_ptr   :: Int
    last_ptr    :: Int
    values      :: Vector{Int}
    indices     :: Vector{Int}
end

Now we need some functions like:

has, rm!, fix!

We first assume that our values are an interval starting with 1 so we need later something which works with different intervals but later.

function has(v::Variable, x::Int)
    if x > length(v.values) || x < 1
        return false
    end
    ind = v.indices[x]
    return v.first_ptr <= ind <= v.last_ptr
end

Then our remove function which I explained at the beginning. Here we don't check whether the value is actually inside the range for speed so whenever we remove a value we should be sure that it isn't already removed.

function rm!(v::Variable, x::Int)
    ind = v.indices[x]
    v.indices[x], v.indices[v.values[v.last_ptr]] = v.indices[v.values[v.last_ptr]], v.indices[x]
    v.values[ind], v.values[v.last_ptr] = v.values[v.last_ptr], v.values[ind]
    v.last_ptr -= 1
end

here we also just set the barriers without checking whether it makes sense because later in backtracking we fix a value several times which normally isn't done in constraint programming as if a value is set it should be set.

function fix!(v::Variable, x::Int)
    ind = v.indices[x]
    v.last_ptr = ind
    v.first_ptr = ind
end

we should also have a function which checks whether a variable is fixed:

function isfixed(v::Variable)
    return v.last_ptr == v.first_ptr
end

Okay now to the actual changes:

We want to have only search_space and not grid and search_space and we build the search_space by simply adding more variables to it.

The internal structure is a simple vector then and the user can have any structure for example a grid as before for the sudoku.

I know these are substantial changes but as mentioned I'm writing this along coding and therefore some bugs and bigger changes will happen that's somehow also the goal of the series to see the changes while they happen instead of following a step by step guide on how to build a constraint solver where everything works :D

Okay we need a addVar! function which adds it to our model and returns the Variable object back to the user who can use it in it's own data structure.

I'm thinking about:

com_grid = Array{CS.Variable, 2}(undef, 9, 9)
for (ind,val) in enumerate(grid)
    if val == 0
        com_grid[ind] = CS.addVar!(com, 1, 9)
    else
        com_grid[ind] = CS.addVar!(com, 1, 9; fix=val)
    end
end

we provide a start and end value and can fix it while creating the variable.

function addVar!(com::CS.CoM, from::Int, to::Int; fix=nothing)
    ind = length(com.search_space)+1
    var = Variable(ind, 1, to-from+1, 1:to-from+1, 1:to-from+1)
    if fix !== nothing
        fix!(var, fix)
    end
    push!(com.search_space, var)
    push!(com.subscription, Int[])
    return var
end

I also changed the init function as we build the search space on the go now:

function init()
    com = CoM()
    com.constraints         = Vector{Constraint}()
    com.subscription        = Vector{Vector{Int}}()
    com.search_space        = Vector{Variable}()
    com.bt_infeasible       = Vector{Int}()
    com.info                = CSInfo(0, false, 0, 0)
    return com
end

For the constraint functions we now not just give the cartesian indices we give a list of variables over which the constraint should hold i.e CS.add_constraint!(com, CS.all_different, com_grid[CartesianIndices((rc:rc,1:9))]) instead of CS.add_constraint!(com, CS.all_different, CartesianIndices((rc:rc,1:9)))

which means that this is our new add_constraint! function:

"""
    add_constraint!(com::CS.CoM, fct, variables)

Add a constraint using a function name and the variables over which the constraint should hold
"""
function add_constraint!(com::CS.CoM, fct, variables)
    current_constraint_number = length(com.constraints)+1
    indices = vec([v.idx for v in variables])
    constraint = Constraint(current_constraint_number, fct, indices)
    push!(com.constraints, constraint)
    for i in indices
        push!(com.subscription[i], current_constraint_number)
    end
end

Attention: This will be changed later based on other problems ;)

Now to a more interesting part as this is unfortunately quite boring to read I assume :/ Let's have a look at the all_different function.

Normally we saved which indices changed, how we pruned (which values got removed) and which cells got fixed. Now as we don't really remove any values we simply move a pointer and do some swapping in the reverse pruning step we can just move the last_ptr to the right (don't need to swap as the ordering is not important) and therefore we only need to save how many values we have pruned but not which ones. We also don't have to save which values we fixed which we only needed in reverse pruning.

For now I will still use a dictionary for changed as I think it's easier to handle.

This at the beginning of all_different

changed = Dict{CartesianIndex, Bool}()
pruned  = Dict{CartesianIndex,Vector{Int}}()
fixed   = Dict{CartesianIndex, Bool}()

gets changed to:

changed = Dict{Int, Bool}()
pruned  = zeros(Int, length(indices))

Then I changed the fixed_vs_unfixed function which had as input the grid which doesn't exist anymore and not_val which is now only part of the user interface but not part of our solver anymore.

There was

if grid[i] != not_val
    push!(fixed_vals, grid[i])

which is now

if isfixed(search_space[i])
    push!(fixed_vals, value(search_space[i]))

which is much easier to read well we have to write the value function :D

function value(v::Variable)
    @assert v.last_ptr == v.first_ptr
    return v.values[v.last_ptr]
end

but that was simple. I check here that it's actually fixed again which we might want to remove when we are sure that everything works.

I encountered some "problems" during the changing process that I want to share and not show you every change I made as that might become boring.

We don't have pval anymore so I decided that each constraint gets a range of values which it operates on instead and all_different now gets the Constraint object and not just the indices. That makes the add_constraint! function a little bit bigger see GitHub

reverse_pruning gets quite short now as we don't have to check anymore which values we removed or fixed in our pruning step. We just have to increase the last_ptr.

So this:

for local_ind in constraint.indices
    if !haskey(constraint_output.pruned, local_ind)
        continue
    end

    if haskey(constraint_output.fixed, local_ind)
        com.grid[local_ind] = com.not_val
    end
    if !haskey(com.search_space, local_ind) && length(constraint_output.pruned[local_ind]) > 0
        com.search_space[local_ind] = Dict{Int,Bool}()
    end
    for pval in constraint_output.pruned[local_ind]
        com.search_space[local_ind][pval] = true
    end
end

is now:

for (i,local_ind) in enumerate(constraint.indices)
    com.search_space[local_ind].last_ptr += constraint_output.pruned[i]
end

I've added an issue to GitHub that we need to be careful if a constraint directly fixes a value and not removes all other values like we do now as then this would not work. Then we also need to move the first_ptr of the variable accordingly.

In our backtracking function we now save the position of last_ptr before we set a value and in the end before return :Infeasible we reset it to what it was before.

We have the fulfills_constraints function which we call before setting a value in all_different but as we don't have the search_space & grid structure anymore it isn't fulfilled as we have set it already. Therefore the function now checks every index which is not the current one.

Checking whether our problem is solved is done by:

if all(v->isfixed(v), com.search_space)
    return :Solved
end

now which takes a bit time compared to length(com.search_space) == 0 but it's okay. We don't call it often.

You remember that I said we care about variables with a range different to 1-xlater? That's now:

So we simply store an offset in our Variable struct. If we have 0-8 the offset is 1. Which means if we want to remove 5. We look at index 5+offset = 6 of the indices vector to get the index of the value where 5 is stored. That's it.

You might think:

• That was hard work

• We should have done that before

Well yes that might be correct but I think we kind of went from a somehow specialized solver to a more abstract solver and we improved the performance ;)

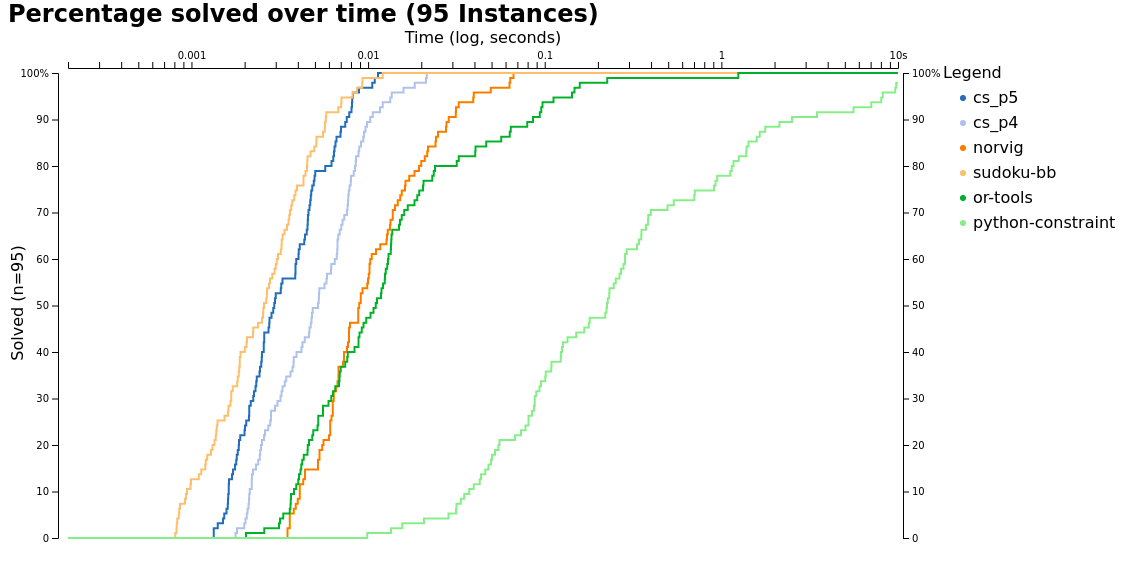
We moved from light blue to dark blue which isn't too bad.

Fix in alldifferent

As mentioned in the last post our all_different constraint only works if we have the same number of indices as number of variables but how about if we need to choose 9 values from 15?

We still check the maximum matching against the number of indices (9) but we need to find

• an even alternating path starting at a free vertex

according to Berge's lemma. A free vertex is now a value which wasn't chosen in the maximum matching. Now we could just try to find all even alternating path starting at a free vertex but that doesn't sound practical so instead we add another node to and connect it in such a way that we can still find all strongly connected components as we do anyway.

As an example:

The upper blue lines would be the even alternating path starting at the free vertex 10 and the two blue lines at the bottom make it to a cycle which will be detected by our strongly connected components.

We don't care about these extra edges when we remove values so we need to check there whether the edge has an end point at the new vertex and if that's the case we ignore it.

Test cases

I've removed the test case with the 42,44,... sudoku as I think it's not very helpful and we could still solve it by having all a range 42-x and remove the odd values 43,45 at the start.

I've added a test which has a normal sudoku but some cells don't have a range from 1-9 but 9-11 or something. This adds more possibilities to solving the sudoku but adds functionality we didn't have before with our build_search_space structure.

What's next?

I'm thinking about solving Killer sudokus next which works with a sum constraint as well as the all_different constraint.

Maybe backtracking shouldn't be implemented as recursion to never run in the problem of getting a recursion limit error.

Should the variable check whether it's feasible to set it? So whenever a variable is fixed it might should call fulfills_constraints itself and return whether it's successful as I think the person who implements constraints shouldn't handle that this directly.

Stay tuned ;)

Here it is:

• Part Six: Backtracking without recursion and beginning of sum constraint

• Part Seven: Speed up of the sum constraint

And as always:

Thanks for reading!

If you enjoy the blog in general please consider a donation via Patreon to keep this project running.

If you have any questions, comments or improvements on the way I code or write please comment here and or write me a mail o.kroeger@opensourc.es and for code feel free to open a PR on GitHub ConstraintSolver.jl

Additionally if you want to practice code reviews or something like that I would be more than happy to send you what I have before I publish. ;)

I'll keep you updated if there are any news on this on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de

Want to be updated? Consider subscribing on Patreon for free