Constraint Solver: Support for linear objectives

Creation date: 2020-01-21

Tags: julia, optimization, constraint-programming

This is part 17 of the series about: How to build a Constraint Programming solver?

In this series I'm building a constraint solver from scratch in Julia.

If you are new to this blog and are interested in constraint programming, there are several posts already waiting for you:

but that is a long list so I'll make a short post again for Part 20. Explaining what I've programmed so far and what is still missing. I'm doing this in my free time but would like to spend more and more time programming this project as well as blogging about it. If you want to support this project and the blog in general I would be amazed if you become a patron. If you do I will create a better/faster blog experience and you will get posts like this two days in advance! Everything will be free forever but if you have some cash to spare -> This might be an option ;)

Special limited offer only for X days... I either just lost your attention or I have it now :D I decided to offer a 1:1 (binary) talk where you can ask me about my work and just chat with me if you're willing to join the Patron 4$ club. ;) This offer exists until the 10th of February.

Implementing support for linear objectives

If you want to just keep reading -> Here you go ;)

Since the last part the solver supports real coefficients but it only supports to minimize/maximize a single variable the next reasonable step is to support linear objective functions in general. As you might remember all the variables are discrete which means we can't minimize something like $0.5x+7.2y$ as of now.

Feel free to check out all the code changes needed to make this possible on GitHub PR #61.

This post explains the needed changes to make it work. At first it seems like an easy problem again as we only need to change the get_best_bound functionality. We only had single_variable_objective here.

Now we add a function called linear_combination_objective into the same file src/objective.jl.

Where we use the fact that we have a linear combination so the maximum sum is adding the maximum terms together which consist of the maximum value for each variable times the coefficient, if the coefficient is positive and otherwise take the minimum value.

In code on Github

function linear_combination_objective(com::CS.CoM, var_idx::Int, val::Int)
    objective = com.objective
    indices = objective.lc.indices
    coeffs = objective.lc.coeffs
    objval = objective.constant
    if com.sense == MOI.MIN_SENSE
        for i=1:length(indices)
            if indices[i] == var_idx
                objval += coeffs[i]*val
                continue
            end
            if coeffs[i] >= 0
                objval += coeffs[i]*com.search_space[indices[i]].min
            else
                objval += coeffs[i]*com.search_space[indices[i]].max
            end
        end
    else # MAX Sense
        for i=1:length(indices)
            if indices[i] == var_idx
                objval += coeffs[i]*val
                continue
            end
            if coeffs[i] >= 0
                objval += coeffs[i]*com.search_space[indices[i]].max
            else
                objval += coeffs[i]*com.search_space[indices[i]].min
            end
        end
    end
    return convert(typeof(com.best_bound), objval)
end

Now we of course need to call that function somewhere which we do in src/MOI_wrapper/objective.jl:

function MOI.set(model::Optimizer, ::MOI.ObjectiveFunction, func::SAF{T}) where T <: Real
    check_inbounds(model, func)
    indices = [func.terms[i].variable_index.value for i=1:length(func.terms)]
    coeffs  = [func.terms[i].coefficient for i=1:length(func.terms)]
    lc = LinearCombination(indices, coeffs)
    model.inner.objective = LinearCombinationObjective(CS.linear_combination_objective, lc, func.constant, indices)
    return
end

Which simply turns @objective(m, Min, 0.5x+7.2y) into the right format we need namely LinearCombinationObjective

mutable struct LinearCombinationObjective{T <: Real} <: ObjectiveFunction
    fct      :: Function
    lc       :: LinearCombination{T}
    constant :: T
    indices  :: Vector{Int} # must exist to update the objective only if one of these changed
end

This is all quite basic stuff. The next problem is that in several cases we now deal with floating objectives/solutions/best bounds whereas everything was constructed with integers only in mind.

Which means we need to use T <: Real for all such cases. JuMP itself normally works on floats which means the default constructor which defines the types later namely ConstraintSolverModel uses Float64 as the default type:

function ConstraintSolverModel(T::DataType=Float64)
    ConstraintSolverModel(
        Vector{Variable}(), # init_search_space
        Vector{Variable}(), # search_space
        Vector{Vector{Int}}(), # subscription
        Vector{Constraint}(), # constraints
        Vector{Int}(), # bt_infeasible
        1, # c_backtrack_idx
        Vector{BacktrackObj{T}}(), # backtrack_vec
        MOI.FEASIBILITY_SENSE, #
        NoObjective(), #
        zero(T), # best_sol,
        zero(T), # best_bound
        Vector{Int}(), # save backtrack id to solution
        CSInfo(0, false, 0, 0, 0), # info
        Dict{Symbol,Any}(), # input
        Vector{TreeLogNode{T}}(), # logs
        SolverOptions() # options
    )
end

this defines the type for the BacktrackObj as well as for TreeLogNode which is only used if we want to keep the full logs (the search tree information).

The solver itself supports different types like Int. If you want to use that you have to use MOI directly for example:

m = CS.Optimizer(; solution_type = Int)
        
x = [[MOI.add_constrained_variable(m, MOI.Integer()) for i=1:9] for j=1:9]
for r=1:9, c=1:9
    MOI.add_constraint(m, x[r][c][1], MOI.GreaterThan(1))
    MOI.add_constraint(m, x[r][c][1], MOI.LessThan(9))
end

In the future JuMP will support other types as well and then everything should for without major/or any changes.

Because every type needs to be consistent we convert the return type of our objectives to the correct type.

Some functions which come in handy here are zero(T), zero(val) and convert(T, val). The first one simply returns the 0 with the type T which means zero(Int) returns a 0 of type Int64 and zero(Float64) returns 0.0 of that type. Instead of writing zero(typeof(val)) you can simply write zero(val). The last function converts a value to the type T and throws an error if this is not possible.

Now we can solve problems like this:

matrix = [
    0 1 0 1
    1 0 1 0
    0 1 0 1
    1 0 1 0
]
m = Model(with_optimizer(CS.Optimizer))
@variable(m, x[1:4], Bin)
for i in 1:4, j in 1:4
    if matrix[i,j] == 1 && i < j
        z = @variable(m, lower_bound = 0.0, upper_bound = 1.0, integer = true)
        @constraint(m, x[i]+x[j]+z == 1.0)
    end
end
weights = [-0.2, -0.1, 0.2, -0.11]
@objective(m, Min, sum(weights.*x))
optimize!(m)
@test JuMP.value(x[4]) == 1
@test JuMP.value(x[2]) == 1
@test JuMP.objective_value(m) ≈ -0.21

Which represents the graph:

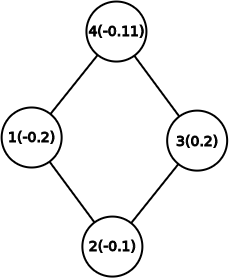
And we want to select vertices in a way that we want to minimize the cost over all vertices such that selected vertices are not connected.

If we select 0 vertices we get a score of 0.0 which is at least better than selecting vertex 3 with a cost of 0.2. A better way is to select the single vertex 1 with a cost of -0.2 but we can't reduce the cost further if we hang on vertex 1. Instead the best solution is to select vertex 2 and 4 and have an objective function of -0.21.

This is one of many problems the constraint solver wasn't able to solve before.

Next up will be:

Better dispatch on functions see PR #63:

Currently each constraint is not perfectly typed as the constraint function is of type ::Function which might lead to worse performance. Additionally there exists a smoother way by using what is used for the MathOptInterface interface anyway.
Support for $\leq$ and $\geq$ constraints. I try to find another nice puzzle or real world problem to solve with all this new stuff implemented then.

I'm also currently trying to finally find the optimum in the last Santa Kaggle challenge which I blogged about before Kaggle Santa Challenge. I hope I manage to finally get it as I kind of know now how it should be possible given all the solutions in the forum. After that I'll make a big post on the Challenge with all my ideas listed and an explanation why some things worked and some didn't. This might take a while :/

This blog lives because of my patreons who help me pay for my server and a little bit of my time. If you want to support this blog as well please consider a donation via Patreon.

If you just want to get notified by new posts you should check out my Twitter profile @opensourcesblog.

New posts:

Thanks for reading and special thanks to my five patrons!

List of patrons paying more than 2$ per month:

Site Wang
Gurvesh Sanghera

Currently I get 10$ per Month using Patreon and PayPal when I reach my next goal of 50$ per month I'll create a faster blog which will also have a better layout:

Code which I refer to on the side
Code diffs for changes
Easier navigation with Series like Simplex and Constraint Programming
- instead of having X constraint programming posts on the home page
And more

If you have ideas => Please contact me!

For a donation of a single dollar per month you get early access to the posts. Try it out at the start of a month and if you don't enjoy it just cancel your subscription before pay day (end of month). Check out Patreon!

Any questions, comments or improvements? Please comment here and/or write me an e-mail o.kroeger@opensourc.es and for code feel free to open a PR/issue on GitHub ConstraintSolver.jl

I'll keep you updated on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de

Want to be updated? Consider subscribing and receiving a mail whenever a new post comes out.

Subscribe to RSS

OpenSourc.ES

Constraint Solver: Support for linear objectives

Implementing support for linear objectives