Constraint Solver Part 7: Sum constraint speed-up

Series: Constraint Solver in Julia

• Part One: Setup and backtracking

• Part Two: Pruning

• Part Three: Pruning+Benchmarking

• Part Four: Alldifferent constraint

• Part Five: Better data structure

• Part Six: Sum constraint first part

This is part 7 of the series about: How to build a Constraint Programming solver?

Last time we introduced the equal sum constraint (eq_sum) and figured out that it isn't that fast to solve a hard killer sudoku with it.

Edit 02.10.2019: I just found out that each cage (colored region) has a all different constraint as well. I don't use that here as I didn't read it :/ but it's also reasonable for the solver and this post that we concentrate on the sum constraint.

Last time we ended up with this if we don't backtrack:

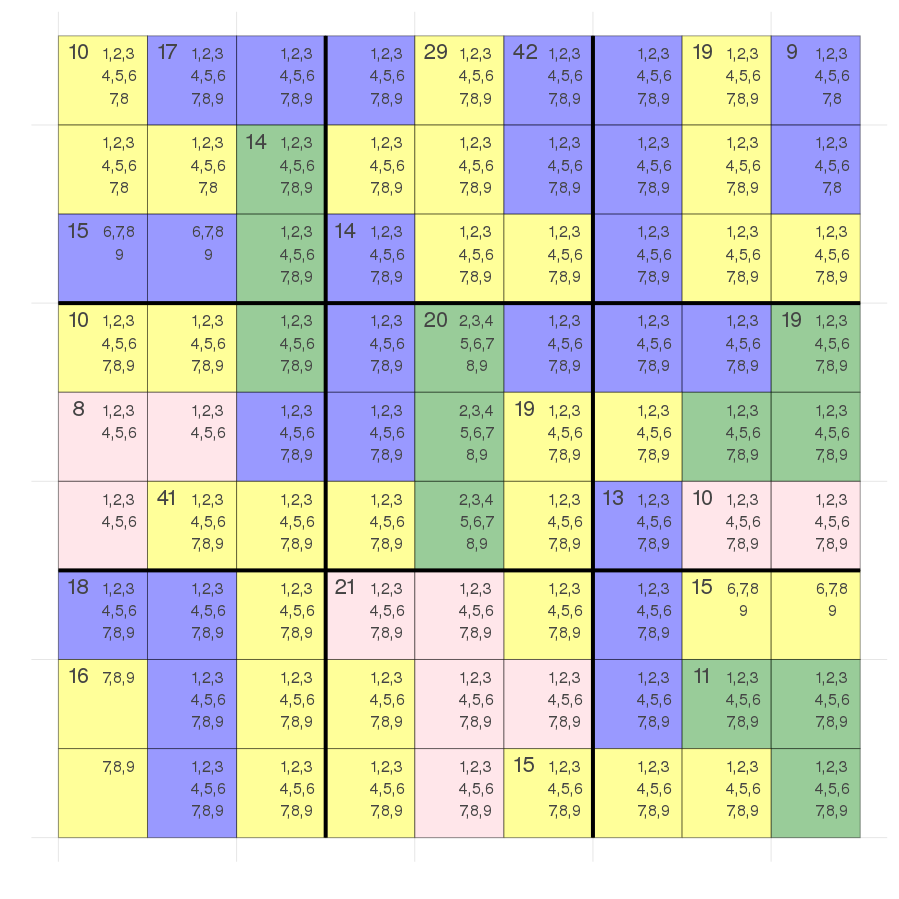
Remark:

• a killer sudoku has the same constraints as a normal sudoku

• plus the constraint that each colored region must add up to the number shown in the top left of that region

I talked about some ideas of how we might be able to further prune the search space:

• Combining sum constraint with all different constraint

  • i.e bottom left 7,8,9 + 7,8,9 should add up to 16 but it is inside same all different => no 8 possible

• Use the sum constraint of row, column or block add up to 45

  • bottom right block: We can have an additional constraint that the red marked cells add up to 9

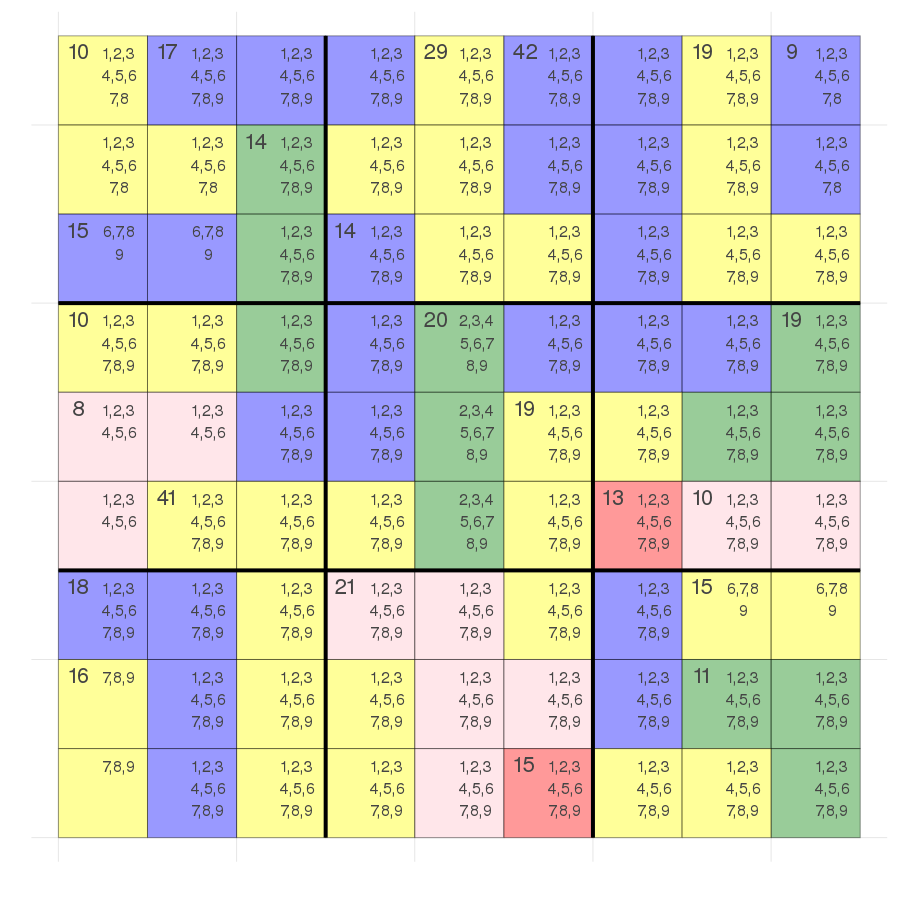
First what is our current benchmark result for this problem? My setup:

• 6 core Intel(R) Xeon(R) CPU E5-1650 0 @ 3.20GHz

• Julia 1.2

julia> @benchmark main(;benchmark=true)
BenchmarkTools.Trial: 
  memory estimate:  44.83 GiB
  allocs estimate:  317941771
  --------------
  minimum time:     42.523 s (18.96% GC)
  median time:      42.523 s (18.96% GC)
  mean time:        42.523 s (18.96% GC)
  maximum time:     42.523 s (18.96% GC)
  --------------
  samples:          1
  evals/sample:     1

and this is the info:

Info: 
pre_backtrack_calls = 77
backtracked = true
backtrack_counter = 87829
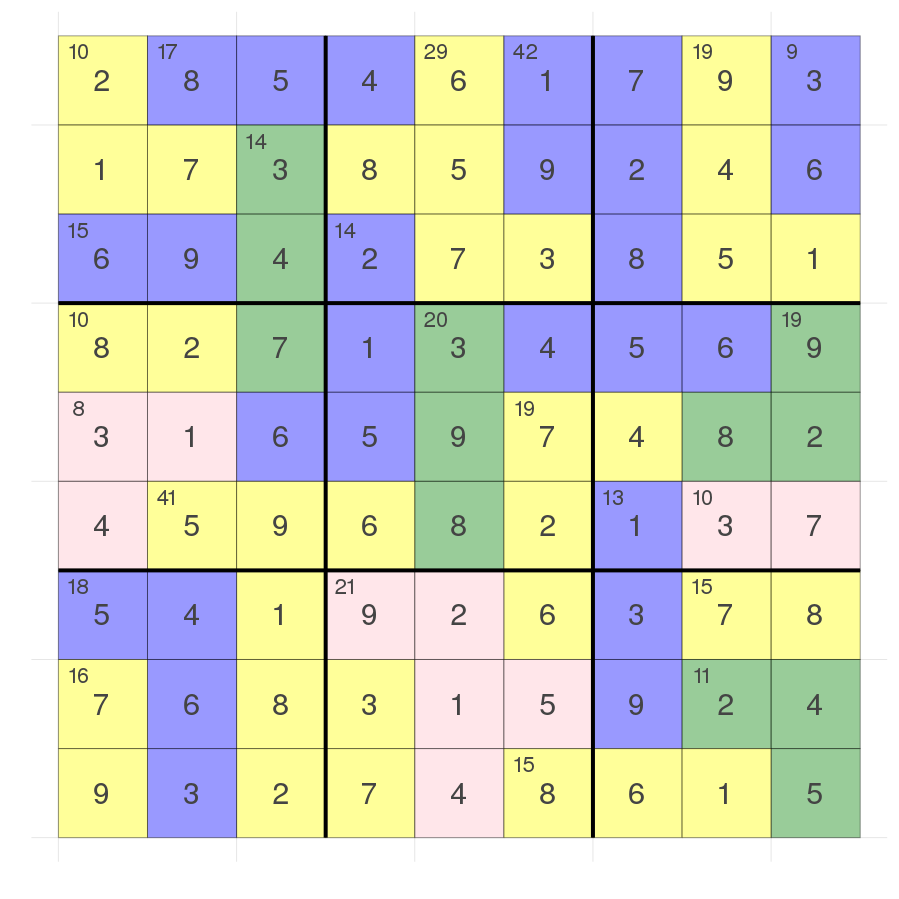
in_backtrack_calls = 4136981

Edit 02.10.2019: I've realized that I never showed the solution to the hard puzzle but I think it might be interesting. As far as I can see the solution does fulfill the actual constraints of killer sudokus (each colored region should have unique digits) as well.

Okay let's start with a very simple version:

If there are only two unfixed variables in a sum constraint we test all options and check whether it's feasible or not i.e if the possibilities are [1,4] and [1,2,3,4] and the sum should equal 5 we currently don't prune anything as we normally only prune the outside values but we clearly can reduce the possibilities of the second variable to [1,4] as well.

We check first how many unfixed variables there are and save the indices (both the normal index of the variable and the local index for pruned).

# if there are only two left check all options
n_unfixed = 0
unfixed_ind = zeros(Int,2)
unfixed_local_ind = zeros(Int,2)
unfixed_rhs = constraint.rhs
li = 0
for i in indices 
    li += 1
    if !isfixed(search_space[i])
        n_unfixed += 1
        if n_unfixed <= 2
            unfixed_ind[n_unfixed] = i
            unfixed_local_ind[n_unfixed] = li
        end
    else
        unfixed_rhs -= value(search_space[i])
    end
end

Then we check whether we have n_unfixed == 2 and if that is the case:

for v in 1:2
    if v == 1
        this, local_this = unfixed_ind[1], unfixed_local_ind[1]
        other, local_other = unfixed_ind[2], unfixed_local_ind[2]
    else
        other, local_other = unfixed_ind[1], unfixed_local_ind[1]
        this, local_this = unfixed_ind[2], unfixed_local_ind[2]
    end
    for val in values(search_space[this])
        if !has(search_space[other], unfixed_rhs-val)
            rm!(search_space[this], val)
            changed[this] = true
            pruned[local_this] += 1
        end
    end
end

This means we iterate through all possibilities for the first variable and check whether the rest is a possibility in the second variable and then we do it the other way around. If the other variable doesn't have the possibility we can remove the possibility from the current checking variable.

This gives us a nice reduction but not enough:

julia> @benchmark main(;benchmark=true)
BenchmarkTools.Trial: 
  memory estimate:  33.59 GiB
  allocs estimate:  244525754
  --------------
  minimum time:     32.301 s (18.77% GC)
  median time:      32.301 s (18.77% GC)
  mean time:        32.301 s (18.77% GC)
  maximum time:     32.301 s (18.77% GC)
  --------------
  samples:          1
  evals/sample:     1

The next obvious step is to reduce it further by checking whether the two variables are also in the same all different constraint.

Then we can remove values from the [7,8,9] + [7,8,9] == 16 case as the 8 obviously can't be chosen but only because of the combination with the all different constraint.

Therefore inside the if n_unfixed == 2 we add:

intersect_cons = intersect(com.subscription[unfixed_ind[1]], com.subscription[unfixed_ind[2]])
is_all_different = false
for constraint_idx in intersect_cons
    if nameof(com.constraints[constraint_idx].fct) == :all_different
        is_all_different = true
        break
    end
end

This gets all constraints for both variables and checks whether there is an all different constraint which connects those two.

Then inside for val in values(search_space[this]) we add

if is_all_different && unfixed_rhs-val == val
    rm!(search_space[this], val)
    changed[this] = true
    pruned[local_this] += 1
    if has(search_space[other], unfixed_rhs-val)
        rm!(search_space[other], val)
        changed[other] = true
        pruned[local_other] += 1
    end
end

as a safety check we check whether both indices still have possible values and if not we return our Infeasible output:

if !feasible(search_space[unfixed_ind[1]]) || !feasible(search_space[unfixed_ind[2]])
    return ConstraintOutput(false, changed, pruned)
end

That gives us another nice speed up:

julia> @benchmark main(;benchmark=true)
BenchmarkTools.Trial: 
  memory estimate:  12.82 GiB
  allocs estimate:  94858954
  --------------
  minimum time:     12.512 s (17.94% GC)
  median time:      12.512 s (17.94% GC)
  mean time:        12.512 s (17.94% GC)
  maximum time:     12.512 s (17.94% GC)
  --------------
  samples:          1
  evals/sample:     1

We can of course do something like this for 3 variables or more but I don't want to bruteforce too much.

Instead I want to think more about the plot I've shown you before:

Here the two red cells should add up to 9 as the bottom right block (as well as all other blocks, rows, cols) adds up to 45 and the red cells plus the block adds up to \(54=13+15+11+15\).

In general I had the following idea:

1. If we have all different constraints and sum constraints

2. Check if we have #variables == #values for all different

3. Compute the sum of all different

4. Compute the sum using sum constraint where all variables are inside this all different constraint

5. Compute the total sum of all sum constraints which have at least one variable inside all different

6. If there are not too many outside variables add a sum constraint

   1. for the outside variables

7. Take care that we don't mess up anything

At the start of solve I call:

# check for better constraints
simplify!(com)

First step in that function:

• check if we have all_different and sum constraints

  • where all different uses every value

b_all_different = false
b_all_different_sum = false
b_sum = false
for constraint in com.constraints
    if nameof(constraint.fct) == :all_different
        b_all_different = true
        if length(constraint.indices) == length(constraint.pvals)
            b_all_different_sum = true
        end
    elseif nameof(constraint.fct) == :eq_sum
        b_sum = true
    end
end

We add constraints during this process but to make it not too complicated we will only work on the current set of constraints.

if b_all_different_sum && b_sum
    n_constraints_before = length(com.constraints)
    for constraint_idx in 1:length(com.constraints)
        constraint = com.constraints[constraint_idx]
        if nameof(constraint.fct) == :all_different
            if length(constraint.indices) == length(constraint.pvals)
            
                ----> ADDING REST here (1)

            end
        end
    end
end

During the following process we want to know the sum of the all different constraint (in our case always sum(1:9) == 45), the sum of sum constraints where all the sums are inside the all different constraint (in_sum) the total sum we compute which means all_diff_sum plus the outside variables (total_sum). We need to keep track of which indices are outside and which indices we checked already.

all_diff_sum = sum(constraint.pvals)
in_sum = 0
total_sum = 0
outside_indices = Int[]
cons_indices_dict = arr2dict(constraint.indices)

If we used a variable already we will remove it from cons_indices_dict such that we don't use any variable inside the all different constraint more than once.

for variable_idx in keys(cons_indices_dict)
    for sub_constraint_idx in com.subscription[variable_idx]

        ----> ADDING REST here (2)
    
    end
end

We only check constraints for now which were already there before we ran simplify!

# don't mess with constraints added later on
if sub_constraint_idx > n_constraints_before
    continue
end

Now we want to check whether we are dealing with a eq_sum constraint:

sub_constraint = com.constraints[sub_constraint_idx]
if nameof(sub_constraint.fct) == :eq_sum
    ----> ADDING REST here (3)
end

We definitely add the rhs to total_sum and then check whether all of the indices of that constraint are inside the all different constraint. If that is the case we add the rhs also to in_sum and delete the variable from cons_indices_dict such that we don't check the same constraint again later which would result in adding too much.

total_sum += sub_constraint.rhs
all_inside = true
for sub_variable_idx in sub_constraint.indices
    if !haskey(cons_indices_dict, sub_variable_idx)
        all_inside = false
        push!(outside_indices, sub_variable_idx)
    else 
        delete!(cons_indices_dict, sub_variable_idx)
    end
end
if all_inside
    in_sum += sub_constraint.rhs
end
break

The break at the end is because we don't want to check other sub constraints if we found one already.

In Rest (1):

# make sure that there are not too many outside indices
if length(outside_indices) < 3
    add_constraint!(com, CS.eq_sum, com.search_space[outside_indices]; rhs=total_sum - all_diff_sum)
end

We should check first whether it still works by running main(;benchmark=false)

This checks whether it gets solved appropriately which is the case. And this is our benchmark run:

julia> @benchmark main(;benchmark=true)                       
BenchmarkTools.Trial:        
  memory estimate:  3.25 GiB 
  allocs estimate:  23988420 
  --------------    
  minimum time:     3.183 s (17.82% GC)   
  median time:      3.198 s (18.05% GC)   
  mean time:        3.198 s (18.05% GC)   
  maximum time:     3.214 s (18.29% GC)   
  --------------                                                      
  samples:          2                                                 
  evals/sample:     1

This looks much better than our starting point but still worse than I hoped it will look like.

Before we might try something else we should check that this actually works and doesn't mess things up. It's always good to think about problems which are different than the ones you currently try to solve.

What if there is a variable inside an all different constraint which is not part of a sum constraint? I know this is never the case in a killer sudoku but our solver should be a general solver so it should still be able to solve it.

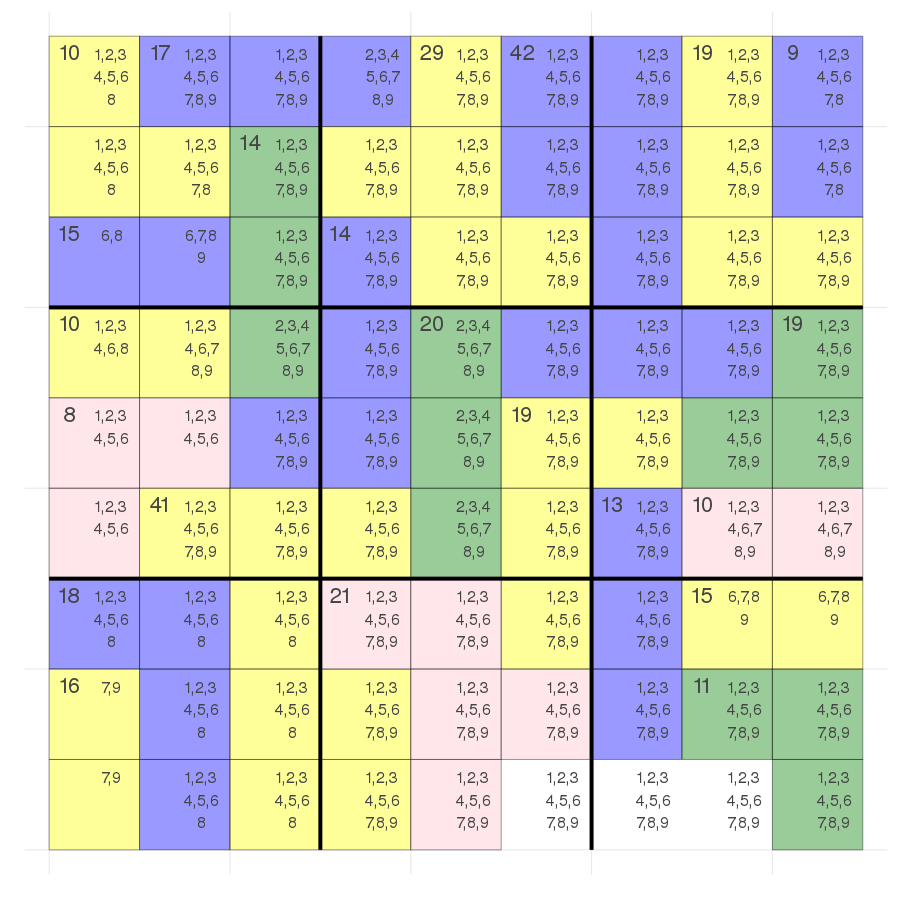
The obvious problem is that we assume that there is a sum constraint for every variable in our all different constraint. What we do is basically saying that the white cells inside the bottom right block add up to 0 instead of we don't know what they add up to.

Therefore we need to check whether each variable is part of a sum constraint and if not we ignore that particular all different constraint.

Two more things for this post:

• Whenever we remove values

  • Check if we removed all values or all but one:

    • Check whether we are still feasible

• Make sure that we fix values when we can in the sum constraint

More on the second one later. I didn't think about it before and it's kind of a bug in the code...

We do the first part of checking inside all_different but not inside eq_sum and we should actually do it inside the Variable.jl file.

Each of the following functions will now return whether the function made the problem infeasible:

• fix!, remove_above!, remove_below!, rm!

We need the com model for checking this so the first parameter will be com for all of those.

The problem is that we want to have ::CS.CoM to specify the type but the type doesn't exist as we have to specify the type of Variable before it. I moved the type declaration into the main file now and include Variable.jl after mutable struct CoM.

If we fix a value we check whether this violates another constraint:

if !fulfills_constraints(com, v.idx, x)
    return false
end

that is the first thing we check in the function and in the end we add a return true.

In general I think it's reasonable to check first before removing anything. This means we have to compute in remove_below! & remove_above! first how many values will be deleted to check whether only a single or no value is left and then check whether it would be feasible before we actually remove values.

This for example is the start of the remove_below! function now:

vals = values(var)
still_possible = filter(v -> v >= val, vals)
if length(still_possible) == 0
    return false, 0
elseif length(still_possible) == 1
    if !fulfills_constraints(com, var.idx, still_possible[1])
        return false, 0
    end
end

Ah and we can set bt_infeasible there as well i.e:

vals = values(var)
still_possible = filter(v -> v >= val, vals)
if length(still_possible) == 0
    com.bt_infeasible[var.idx] += 1
    return false, 0
elseif length(still_possible) == 1
    if !fulfills_constraints(com, var.idx, still_possible[1])
        com.bt_infeasible[var.idx] += 1
        return false, 0
    end
end

Later if we remove a value we call:

if !rm!(com, variable, value)
    # return INFEASIBLE
end
# otherwise add to prune

Now the next point is the following: if we have variables a and b and a is fixed to 5 and b is either 1 or 2 and the sum is 6.

We can easily fix the value of b to 1 but we currently don't. This is due to the case that \(5+2 \geq 6\) where 2 is the maximum value so it seems to be okay if there are other values which might be able to reduce the sum.

Therefore in the end instead of checking if there are two unfixed variables we also check if there is a single unfixed variable.

if n_unfixed == 1
    if !has(search_space[unfixed_ind[1]], unfixed_rhs)
        com.bt_infeasible[unfixed_ind[1]] += 1
        return ConstraintOutput(false, changed, pruned, pruned_below)
    else
        changed[unfixed_ind[1]] = true
        still_feasible, pr_below, pr_above = fix!(com, search_space[unfixed_ind[1]], unfixed_rhs)
        if !still_feasible
            return ConstraintOutput(false, changed, pruned, pruned_below)
        end
        pruned[unfixed_local_ind[1]] += pr_above
        pruned_below[unfixed_local_ind[1]] += pr_below
    end
elseif n_unfixed == 2 # ...

This is the first time that we actually fix a variable directly. Hope you can remember that if we fix a variable we move two pointers:

Therefore in reverse pruning we also need to move the first_ptr now. I created a new pruned_below vector to save when we pruned from the other direction.

I'm not too sure whether there might be better ways to compute the next variable to branch on instead of the bt_infeasible counter. For this problem it doesn't seem to be the ideal choice but still better than the normal branch on lowest number of possibilities one.

julia> @benchmark main(;benchmark=true, backtrack=true)
BenchmarkTools.Trial: 
  memory estimate:  3.57 GiB
  allocs estimate:  27452510
  --------------
  minimum time:     3.421 s (16.52% GC)
  median time:      3.489 s (17.88% GC)
  mean time:        3.489 s (17.88% GC)
  maximum time:     3.556 s (19.19% GC)
  --------------
  samples:          2
  evals/sample:     1

That is the end result for the hard killer sudoku now but it's quite good that for the easy one from wikipedia we don't need backtracking ;)

I've added some test cases only for the sum constraint to make sure that it does what it should. This way I observed the problem with not fixing a variable.

The last part solves issue #7 A variable can't be fixed in a constraint

What's up next time?

Good question. I'm thinking about:

• Graph coloring

• scheduling problems (check feasibility first)

• getting all solutions

• being able to optimize (will be a harder one based on my current DFS implementation :/)

• Element constraint

Maybe you have some ideas: Please comment!

Stay tuned ;)

A new post is out: Part 8: UI refactoring and bugfix of sum constraint

And as always:

Thanks for reading and special thanks to my first two patrons!

If you want to have early access to the next posts as well and enjoy the blog in general please consider a donation via Patreon to keep this project running.

If you have any questions, comments or improvements on the way I code or write please comment here and or write me a mail o.kroeger@opensourc.es and for code feel free to open a PR on GitHub ConstraintSolver.jl

Additionally if you want to practice code reviews or something like that I would be more than happy to send you what I have before I publish. ;)

I'll keep you updated if there are any news on this on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de

Want to be updated? Consider subscribing on Patreon for free