Constraint Solver Part 2: Pruning

Series: Constraint Solver in Julia

• Part One: Setup and backtracking

This is part 2 of the series about: How to build a Constraint Programming solver?

Edit: I finished part 5 now so keep on reading ;)

The first part got more attention in the first two days than I thought. Thanks for that ;) If you want to keep on notified about updates the best thing is to follow the blog on Twitter @Opensourcesblog.

In this post I'll use a different Sudoku than last time as the last time turned out to be relatively easy:

grid[1,:] = [0 0 0 0 0 0 0 0 0]
grid[2,:] = [0 1 0 6 2 0 0 9 0]
grid[3,:] = [0 0 2 0 0 9 3 1 0]
grid[4,:] = [0 0 4 0 0 6 0 8 0]
grid[5,:] = [0 0 8 7 0 2 1 0 0]
grid[6,:] = [0 3 0 8 0 0 5 0 0]
grid[7,:] = [0 6 9 1 0 0 4 0 0]
grid[8,:] = [0 8 0 0 7 3 0 5 0]
grid[9,:] = [0 0 0 0 0 0 0 0 0]

In the current version I have the following benchmark results:

julia> @benchmark main(;benchmark=true)
BenchmarkTools.Trial: 
  memory estimate:  686.05 MiB
  allocs estimate:  19347707
  --------------
  minimum time:     882.354 ms (12.26% GC)
  median time:      953.116 ms (12.70% GC)
  mean time:        940.299 ms (13.98% GC)
  maximum time:     981.150 ms (19.88% GC)
  --------------
  samples:          6
  evals/sample:     1

Info: I've added the ;benchmark parameter to my current script to avoid output if benchmarking.

In this post we want to bring it down to something around 15ms but to do that we first must understand why the current version is slow. I mean if we call 0.9s slow but based on my experience it is, as I know that we can improve it much more.

There are several points:

• We are currently not solving it like a human being

  • This doesn't necessarily have to be our goal if we find a better alternative but might give us some hints

• We only fix the basics and then we do some kind of trial and error

Let's have a look at the search space without backtracking

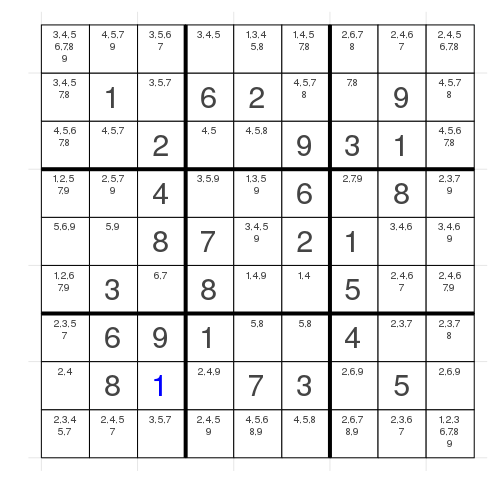
We fix a single number and 54 spots are still open. The backtrack function is called 62264 times. That is a crazy amount. Now we could try to think about how we remove more values from the search space before we start the backtracking and we will do that in the next post.

For this post we try to prune (remove values) while we are doing backtracking.

Before we start with that I want to do some small things I saw after publishing the post:

1. I want to have some information about the solve call like whether backtracking was needed, how many constraint calls we had before backtracking and how often the backtracking function was called.

2. I sometimes only wrote [] instead of Int[] for example.

3. At the moment sometimes a constraint is called even though nothing changed since last time.

To Point #1:

mutable struct CSInfo
    pre_backtrack_calls :: Int
    backtracked         :: Bool
    backtrack_counter   :: Int
end

function Base.show(io::IO, csinfo::CSInfo)
    println("Info: ")
    for name in fieldnames(CSInfo)
        println(io, "$name = $(getfield(csinfo, name))")
    end
end

Added before mutable struct CoM and inside a info :: CSInfo. We fill that in the build_search_space and then increment the counters in our code.

The show function is a custom function for displaying the values inside the struct. After solving I call @show com.info (if benchmark is set to false)

and get

Info: 
com.info = pre_backtrack_calls = 30
backtracked = true
backtrack_counter = 61264

To Point #2:

This is very minor so you can do that yourself or see in my code.

To Point #3:

Our current behavior is:

• We call every constraint once and save which indices changed

• For the changed indices we call the corresponding functions again

• Do that until nothing changed.

Now it might be the case that we fix some value in row one and then call the function for the row constraint again and this time two cells get fixed. They both have the same block and row constraint for example but a different column constraint.

What we are doing at the moment is we call the row constraint twice and the block constraint twice even if in between nothing changed. That's quite stupid.

I'm talking about this code:

while length(com.changed) > 0 && feasible
    first_changed = collect(keys(com.changed))[1]
    delete!(com.changed, first_changed)
    constraints = com.constraints[com.subscription[first_changed]]
    for constraint in constraints
        funcname, indices = constraint
        if findfirst(v->v == com.not_val, com.grid[indices]) === nothing 
            continue
        end
        com.info.pre_backtrack_calls += 1
        feasible = funcname(com, indices)
        if !feasible
            break
        end
    end
end

Link to the lines on GitHub

One step before: At the moment the constraints always just depend on the name and the indices and this might always be the case but maybe not so I want to make a struct for the Constraint.

mutable struct Constraint
    idx                 :: Int
    fct                 :: Function
    indices             :: Union{CartesianIndices,Vector{CartesianIndex}}
end

Then change constraints :: Vector{Tuple} to Vector{Constraint} the same in build_search_space and in adding_constraint we will have:

current_constraint_number = length(com.constraints)+1
constraint = Constraint(current_constraint_number, fct, indices)
push!(com.constraints, constraint)

at the beginning. (I also changed func to fct). Then in solve we need do some changes as well i.e:

for constraint in com.constraints
        if findfirst(v->v == com.not_val, com.grid[constraint.indices]) === nothing 
            continue
        end
        com.info.pre_backtrack_calls += 1
        feasible = constraint.fct(com, constraint.indices)

As long as we actually only need the indices I just give the function the indices here but I think it's still more useable than the Tuple.

Okay now the real stuff. We have the indices of the cells we fixed and want to get the constraints corresponding to that and each constraint should be only called once. If something changed afterwards we will add the constraint again to our list.

constraint_idxs_dict = Dict{Int, Bool}()
for ind in keys(com.changed)
    for constraint in com.constraints[com.subscription[ind]]
        constraint_idxs_dict[constraint.idx] = true
    end
end
empty!(com.changed)

This dictionary takes care that we don't have the same constraint more than once.

Now we actually need the indices:

constraint_idxs = collect(keys(constraint_idxs_dict))
changed_constraints = com.constraints[constraint_idxs]
con_counter = 1

Instead of using the counter we could also pop a constraint but I'm not a fan of that atm. Now instead of checking whether that changed dict is empty we check whether our new constraint_idxs_dict is empty:

while length(constraint_idxs_dict) > 0 && feasible
    constraint = changed_constraints[con_counter]
    con_counter += 1
    delete!(constraint_idxs_dict, constraint.idx)

and then:

if findfirst(v->v == com.not_val, com.grid[constraint.indices]) === nothing 
        continue
    end
    com.info.pre_backtrack_calls += 1
    feasible = constraint.fct(com, constraint.indices)
    if !feasible
        return :Infeasible
    end

At the moment we don't add anything back to constraint_idxs_dict so we should do:

for ind in keys(com.changed)
    for constraint in com.constraints[com.subscription[ind]]
        if !haskey(constraint_idxs_dict, constraint.idx)
            constraint_idxs_dict[constraint.idx] = true
            push!(changed_constraints, constraint)
        end
    end
end
empty!(com.changed)

but we will change that a bit later ;)

Status: Solved

(v1.2) pkg> test ConstraintSolver
  Updating registry at `~/.julia/registries/General`
  Updating git-repo `https://github.com/JuliaRegistries/General.git`
   Testing ConstraintSolver
 Resolving package versions...
    Status `/tmp/jl_7PC8Ng/Manifest.toml`
  [e0e52ebd] ConstraintSolver v0.1.0 [`~/Julia/ConstraintSolver`]
  [2a0f44e3] Base64  [`@stdlib/Base64`]
  [8ba89e20] Distributed  [`@stdlib/Distributed`]
  [b77e0a4c] InteractiveUtils  [`@stdlib/InteractiveUtils`]
  [56ddb016] Logging  [`@stdlib/Logging`]
  [d6f4376e] Markdown  [`@stdlib/Markdown`]
  [9a3f8284] Random  [`@stdlib/Random`]
  [9e88b42a] Serialization  [`@stdlib/Serialization`]
  [6462fe0b] Sockets  [`@stdlib/Sockets`]
  [8dfed614] Test  [`@stdlib/Test`]
[ Info: Backtracking is turned off.
    ....
Test Summary: | Pass  Total
Sudoku        |    8      8
   Testing ConstraintSolver tests passed

Okay that looks good. That's why we have test cases ;)

We still get the same output:

Info: 
com.info = pre_backtrack_calls = 30
backtracked = true
backtrack_counter = 61264

and don't ask me why com.info = is printed in the second line.

There nothing changed but conceptually the new thing is better.

Now to the actual topic of the post :D

Oh wait one last thing:

In our all_different constraint we currently check only whether setting a value to an index is still feasible for the current constraint but not whether it satisfies the other constraints and as I mentioned in the first post: We never want to look for a solution if we could already know that there is none.

Therefore instead of writing:

if in(fixed_vals_set, only_value)
    @warn "The problem is infeasible"
    return false
end

Link to lines on GitHub

before setting the value with com.grid[i] = only_value we should run:

# check whether this is against any constraint
feasible = fulfills_constraints(com, i, only_value)
if !feasible
    @warn "The problem is infeasible"
    return false
end

and define fulfills_constraints inside ConstraintSolver.jl.

function fulfills_constraints(com::CS.CoM, index, value)
    constraints = com.constraints[com.subscription[index]]
    feasible = true
    for constraint in constraints
        feasible = constraint.fct(com, constraint.indices, value)
        if !feasible
            break
        end
    end
    return feasible
end

Okay now the real thing:

We want to call the constraint function whenever we set a value inside our backtracking function because this will reduce the search space quite a bit.

Basically after com.grid[ind] = pval GitHub Line

for (cidx, constraint) in enumerate(constraints)
    feasible = constraint.fct(com, constraint.indices)
    if !feasible
        break
    end
end

The problem with that approach is that our problem now becomes Infeasible and we get a lot of those:

┌ Warning: The problem is infeasible
└ @ ConstraintSolver ~/Julia/ConstraintSolver/src/all_different.jl:27
┌ Warning: The problem is infeasible
└ @ ConstraintSolver ~/Julia/ConstraintSolver/src/all_different.jl:27
┌ Warning: The problem is infeasible
└ @ ConstraintSolver ~/Julia/ConstraintSolver/src/all_different.jl:27
┌ Warning: The problem is infeasible
└ @ ConstraintSolver ~/Julia/ConstraintSolver/src/all_different.jl:27

Okay first about that part: We want to remove output when called from backtracking so we use a parameter logs with default true and false when called from the backtracking function.

Then write logs && @warn "The problem is infeasible" which is kind of a short if.

Okay now about: Why is the problem infeasible? The problem is that we remove values from our search space but if the current track in backtracking is getting reverted we don't add them back to our search space. Therefore we remove too many values until there are no values left and the problem can't be solved anymore.

Therefore we should keep track what we have changed and I use a ConstraintOutput struct for that:

mutable struct ConstraintOutput
    feasible            :: Bool
    idx_changed         :: Dict{CartesianIndex, Bool}
    pruned              :: Dict{CartesianIndex,Vector{Int}}
    fixed               :: Dict{CartesianIndex, Bool}
end

I also don't want to have the com.changed dictionary in our model structure anymore as only the solve function cares about it and instead we have a current changed dictionary in each ConstraintOutput. We want to know which values we removed from the search space (pruned) and which indices got fixed.

At the beginning of our all_different constraint:

changed = Dict{CartesianIndex, Bool}()
pruned  = Dict{CartesianIndex,Vector{Int}}()
fixed   = Dict{CartesianIndex, Bool}()

and instead of return false or return true we have:

return ConstraintOutput(false/true, changed, pruned, fixed)

The com.changed gets changed and after each delete!(com.search_space[i], X)

we add a:

push!(pruned[i], X)

and also a pruned[i] = Int[] for initialization.

After changed[i] = true we also have fixed[i] = true as we later want to set changed whenever something happened not only if we fixed a value. At the moment we don't care about that as our implementation only works on fixed values so it will not be able to prune more if the search space was just reduced. (This will be the case in the next post)

We have to do some changes in solve as we not only return feasible now but an object.

So write something like:

constraint_output = constraint.fct(com, constraint.indices)
if !constraint_output.feasible
    feasible = false
    break
end

and as we don't have com.changed anymore we add

changed = Dict{CartesianIndex, Bool}()

at the very beginning of solve and merge new changes into that with:

merge!(changed, constraint_output.idx_changed)

Instead of adding the changes to constraint_idxs_dict using com.changed after each call we now do:

for ind in keys(constraint_output.idx_changed)
    for constraint in com.constraints[com.subscription[ind]]
        if !haskey(constraint_idxs_dict, constraint.idx)
            constraint_idxs_dict[constraint.idx] = true
            push!(changed_constraints, constraint)
        end
    end
end

Short recap after changing every feasible to ConstraintOutput. What do we want to do again? Well, we now save everything that we changed in each constraint call and if the branch (one track in backtracking) turned out to be infeasible we want to reset it to what we had before like nothing happened. Something like denying that we went down that stupid path.

Basically instead of:

status = rec_backtrack(com)
if status == :Solved
    return :Solved
end

we need a

# we changed the search space and fixed values but didn't turn out well
# -> move back to the previous state
reverse_pruning!(com, constraints, constraint_outputs)

Info: The ! indicates that this function changes the first input parameter. (I should be more consistent with that...)

As we had several constraint propagation calls we need a vector constraint_outputs instead of just constraint_output:

constraint_outputs = ConstraintOutput[]
for (cidx, constraint) in enumerate(constraints)
            constraint_output = constraint.fct(com, constraint.indices; logs = false)
            push!(constraint_outputs, constraint_output)

and now code the reverse_pruning function:

function reverse_pruning!(com, constraints, constraint_outputs)
    for cidx = 1:length(constraint_outputs)
        constraint = constraints[cidx]
        constraint_output = constraint_outputs[cidx]
        for local_ind in constraint.indices
            if !haskey(constraint_output.pruned, local_ind)
                continue
            end

            if haskey(constraint_output.fixed, local_ind)
                com.grid[local_ind] = com.not_val
            end
            if !haskey(com.search_space, local_ind) && length(constraint_output.pruned[local_ind]) > 0
                com.search_space[local_ind] = Dict{Int,Bool}()
            end
            for pval in constraint_output.pruned[local_ind]
                com.search_space[local_ind][pval] = true
            end
        end
    end
end

We iterate over each index that has been pruned (fixed is also pruned). Then add it to the search space again: If we removed everything from the search space for an index we also need to create a dictionary again such that we can fill that.

Now the important part of the backtrack function looks like this:

# value is still possible => set it
com.grid[ind] = pval
constraint_outputs = ConstraintOutput[]
for (cidx, constraint) in enumerate(constraints)
    constraint_output = constraint.fct(com, constraint.indices; logs = false)
    push!(constraint_outputs, constraint_output)
    if !constraint_output.feasible
        feasible = false
        break
    end
end
if !feasible
    continue
end

status = rec_backtrack(com)
if status == :Solved
    return :Solved
else 
    # we changed the search space and fixed values but didn't turn out well
    # -> move back to the previous state
    reverse_pruning!(com, constraints, constraint_outputs)
end

Can you spot the missing piece? At the moment we still get Infeasible.

We also have to reverse pruning when we pruned but it turned out to be infeasible.

So we need

if !feasible
    reverse_pruning!(com, constraints, constraint_outputs)
    continue
end

and now: Tadaa!!!

Solved and the very nice thing:

Info: 
com.info = pre_backtrack_calls = 30
backtracked = true
backtrack_counter = 154

Only 154 backtrack calls instead of over 60,000.

I'm ready for some benchmarking:

julia> @benchmark main(;benchmark=true)
BenchmarkTools.Trial: 
  memory estimate:  4.47 MiB
  allocs estimate:  90668
  --------------
  minimum time:     3.795 ms (0.00% GC)
  median time:      4.295 ms (0.00% GC)
  mean time:        5.499 ms (17.86% GC)
  maximum time:     74.788 ms (93.63% GC)
  --------------
  samples:          909
  evals/sample:     1

Isn't that awesome? It's even better than the 15ms I said at the beginning ;)

That is a 170x improvement on the mean time.

How about our test cases? Yes still works.

Okay I think we should add something to our test cases just to be sure that we are not only solving Sudoku with this.

As Julia is 1 indexed it sometimes gets too easy to not too see some bugs when we have 0 indexed input. So we create a Sudoku with 0-8 and -1 as the not_val and one Sudoku which has the numbers 42, 44, and so on.

I also move CS.build_search_space(com, grid,[1,2,3,4,5,6,7,8,9],0) out of the add_sudoku_constr!(com, grid) function as it isn't really a constraint.

Both new tests pass so it's ready ;)

Let's have a look at the video from the last post:

This is an ongoing series about: How to build a constraint solver?

• Part 1: Idea of how to build a Constraint Solver in Julia

• Part 3: More pruning and benchmarking

Thanks for reading!

If you have any questions, comments or improvements on the way I code or write please comment here and or write me a mail o.kroeger@opensourc.es and for code feel free to open a PR on GitHub ConstraintSolver.jl

Additionally if you want to practice code reviews or something like that I would be more than happy to send you what I have before I publish. ;)

I'll keep you updated if there are any news on this on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de

If you enjoy the blog in general please consider a donation via Patreon to keep this project running.

Want to be updated? Consider subscribing and receiving a mail whenever a new post comes out.

Enter your email

Powered by Buttondown.