First approach for the Kaggle Santa 2019 challenge

Creation date: 2019-11-29

Tags: julia, optimization, kaggle

Okay here it is: I'm waiting for it like almost a year... The new Santa Kaggle Challenge.

This year is a special year for me in that challenge. Normally I try to compete with all my time I have and get the best possible score I can achieve and maybe blog about it when it is all over.

But this year I blog about it while competing. I think it is more interesting for people to read the results in between instead of just the polished end result. I know that everyone can copy it now and I'll not win this challenge but I never did anyway :D

Maybe I can get a discussion medal with it...

Before we start I also want to thank my patrons again because it wouldn't be that awesome without them. Normally you get posts 2 days earlier when you support me but this is against the Kaggle rules so everyone gets it as soon as I've finished writing.

Let's start:

  1. The problem
  2. First steps for each Kaggle competition:
  3. My ideas
    1. Hungarian method
    2. Upgrading families
    3. What's next?

The problem

Some families are allowed to visit the workshop of Santa. Amazing news for 5,000 families. Good for them I would say ;) His workshop is probably quite big but to be not too crowded per day only 300 people can visit the workshop and it isn't reasonable with less than 125. Santa decided to open the workshop for 100 days. The families are super excited to see all the stuff but some days fit better than the others so they are ranked and sent to Santa in advance.

Basically the problem is: How to match each family to a day?

Of course Santa is Santa and therefore wants to be fair so if a family doesn't get their best choice they should have something for it but Santa can't produce more stuff so this time it's just cash, food and a helicopter ride. Yes you heard that right: A north pole helicopter ride. Oh man that sounds ... Okay got distracted here.

Now you can see that this costs money for Santa and you know the world we live in: He wants to minimize his expenses.

Additionally there is some non-linear cost which is called accounting penalty and it's a complicated formula but I trust the Santa's accountants so should be correct ;) (Now there was actually a bug on the evaluation page before).

\[ \text{accounting penalty } =\sum_{d=100}^{1} \frac{\left(N_{d}-125\right)}{400} N_{d}^{\left(\frac{1}{2}+\frac{|N_{d}-N_{d+1}|}{50}\right)} \]

Where \(d\) is the day before Christmas so we are counting towards X-mas here. \(N_d\) is the number of people attending on that day and because we are counting down \(N_{d+1}\) is number of people attending the day before.

Now let's have a deeper look into the other costs which are described here:

If the family gets their first choice for the workshop tour Santa doesn't have to pay anything. Otherwise we have the preference costs:

Basically: No matter what: You win ;)

We are here to help Santa though so we need to reduce his costs.

First steps for each Kaggle competition:

I found this one quite interesting: Santa finances: A closer look at the costs.

My ideas

Hungarian method

In general it is a matching problem which got me thinking that the Hungarian method might be a good starting point. I implemented it two years ago and you can read it here.

This time I'll just use the Julia package Hungarian.jl as it's easier for you to install and it now has a very similar speed to my version.

> julia
julia> ] add Hungarian

Okay now my idea was that we simply put 50 families into each day and hope that it fits the hard constraint of \(125 \leq N_d \leq 300\). Most families have 4 people which you can also see in the Santa finances notebook so I guessed it might work.

This is of course just a rough estimation but if 50 families would be correct for each day this would be optimal for the preference cost and we shouldn't be too bad for the accounting as the fluctuation between two days should be okay.

We need to create a weight matrix first but maybe a small recap on the Hungarian method: It finds the minimum weighted bipartite matching. Bipartite because we connect families to days and weighted because we have the different costs associated to the choices and the actual assigned day.

The matrix needs to be square which is the reason why I duplicated the days 50 times for the 50 spots in each day.

Let's create a julia file: hungarian_test.jl:

using Hungarian, CSV, DataFrames

function get_choice_cost(choice, n)
    if choice == 0
        return 0
    elseif choice == 1
        return 50
    elseif choice == 2
        return 50+9*n
    elseif choice == 3
        return 100+9*n
    elseif choice == 4
        return 200+9*n
    elseif choice == 5
        return 200+18*n
    elseif choice == 6
        return 300+18*n
    elseif choice == 7
        return 300+36*n
    elseif choice == 8
        return 400+36*n
    elseif choice == 9
        return 500+(36+199)*n
    else
        return 500+434*n
    end
end

We need the packages for the Hungarian method itself and for reading the data.

The first function assigns a cost to a choice rank and the number of people we have in a family.

Getting the weights for the cost matrix: We want to create a 5000x5000 matrix and each row represents a family and each column a day (actually 50 columns together represent one day)

function get_weights()
    dff = CSV.read("family_data.csv")

    # preference cost matrix
    preference_mat = zeros(Int, (5000, 5000))
    # first fill every column with the maximum cost for that family
    for row in eachrow(dff)
        preference_mat[row[:family_id]+1,:] .= get_choice_cost(10, row[:n_people])
    end
    
    for row in eachrow(dff)
        # choice cost depends on "how good is the choice?" and on how many people attend
        for i = 0:9
            choice = row[Symbol("choice_"*string(i))]
            choice_cost = get_choice_cost(i, row[:n_people])
            for k=(choice-1)*50+1:choice*50
                preference_mat[row[:family_id]+1, k] .= choice_cost
            end
        end
    end
    return preference_mat
end

We first read the data which has the columns: family_id, choice_i, n_people for \(i=0,...,9\).

I set all weights to 0 first and then for each family I set the highest cost which is choice_10 or basically if the family doesn't get a day out of their Top 10.

Afterward I iterate over all rows (over all family ids) and for the Top 10 choices I get the cost and fill it into the preference matrix for the day corresponding to that choice (always 50 days) for each choice. For the non Julian folks out there I might should mention that .= is for broadcasting and very importantly that julia starts is one index based. The family id is 0 index based and the days are from 1 to 100.

That's all we need to run:

function main()
    weights = get_weights()

    assignment, cost = hungarian(weights)
    println("preference cost: ", cost)
    assigned_day = div.(assignment .- 1, 50).+1
    dfs = DataFrame(family_id = 0:4999, assigned_day = assigned_day)

    CSV.write("hungarian_blog.csv", dfs)
end

assigned_day = div.(assignment .- 1, 50).+1 translates the days back to the 1-100 format.

The preference cost is 142850 and I also wrote a general score script which I'll upload later and get a total score of ~144287.1.

So an accounting cost of a bit over 1400 which is roughly 1% of the total cost.

How good is that in the leader board? Currently (28.11.2019 9:33 (UTC+1)) that is rank 39 and about 14 hours ago it got me into the Top 15 with a small change ;) Well it's the start of the challenge so a lot of people start just now.

The small change was that instead of having 50 families per day I had more families just the day before christmas as that is the top choice for a lot of families and that got me a score of ~111,000 but the code isn't that nice :D So I'll proceed with this one for now and will improve on the other on a different day.

Okay I have another hour before I have to go to university so what was next?

Upgrading families

As mentioned before every day has 50 families so roughly 200 people but probably we can upgrade some families to a better day so that some days have 49 families and others 51 and doing that over and over but always have a look at the hard constraint of between 125 and 300 people per day.

I call that upgrade.jl: I include the score.jl file there which I didn't explain yet but it's not interesting so you can see in in my GitHub repo once everything is tidied up and it shouldn't be hard to implement your own version anyway.

function upgrade(sub_file)
    preference_mat = get_preference_mat();

    dff = CSV.read("family_data.csv")
    dfs = CSV.read(sub_file)
    people_per_day = zeros(Int, 100)
    df_joined = join(dff, dfs, on=:family_id)
    for row in eachrow(df_joined)
        people_per_day[row[:assigned_day]] += row[:n_people]
    end

Just reading the data join it and compute the number of people per day. We only want to change something if we improve the score so let's get the current score first:

old_score = score(preference_mat, dff, dfs)
println("Start: ", old_score)
old_accounting_cost = accounting_cost(people_per_day)
println("old_accounting_cost: ", old_accounting_cost)
assigned_days = df_joined[:,:assigned_day]
day_full = zeros(Bool, 100)

I have an extra function for the accounting cost to be faster in computing whether the score improved or not. The day_full

Oh we need a visualization of something :D

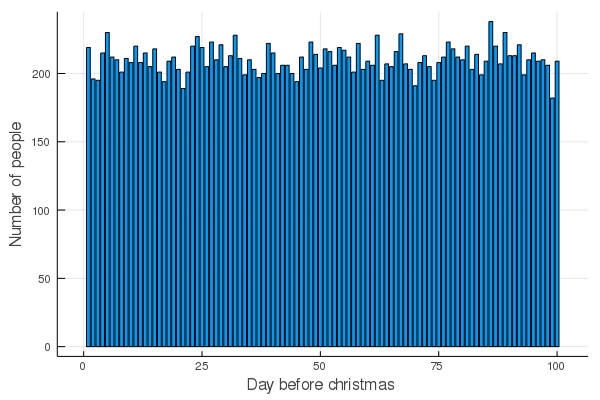
People per day

Now for each family I just try all other days and check whether there is an improvement. It's soo fast I don't have to do something special :D

changed = true
while changed 
    changed = false
    for row_id = 1:5000
        current_day = dfs[row_id, :assigned_day]

        for best_day in 1:100
            if best_day == current_day
                continue
            end

these are the loops so for every family iterate over all days and if it isn't the current day do something. We do this as long as we improve which is the reason for the while changed loop.

Then we check the hard constraints:

n_people = df_joined[row_id, :n_people]

if people_per_day[current_day] - n_people >= 125
    if people_per_day[best_day] + n_people <= 300

and after that we compute the new score.

people_per_day[current_day] -= n_people
people_per_day[best_day] += n_people
new_accounting_cost = accounting_cost(people_per_day)
new_score = old_score - old_accounting_cost - preference_mat[current_day, row_id] + preference_mat[best_day, row_id] + new_accounting_cost

we upgraded n_people from the current day to a better day (shouldn't call it best here...). The new score is the old preference cost - the cost for the current day + the cost for the new day and a new accounting cost.

improvement = old_score-new_score
if improvement > 0 
    current_day = best_day
    assigned_days[row_id] = best_day
    dfs_new = DataFrame(family_id = df_joined[:,:family_id], assigned_day=assigned_days)
    dfs = dfs_new
    df_joined = join(dff, dfs, on=:family_id)
    old_score = new_score
    old_accounting_cost = new_accounting_cost
    CSV.write("best_upgrade.csv", dfs)
    println("New score: ", new_score)
    println("Accounting cost: ", new_accounting_cost)
    changed = true
else
    # reset
    people_per_day[current_day] += n_people
    people_per_day[best_day] -= n_people
end

I was too stupid to change the dataframe which is the reason why I create a new one every time :/ but as I said it's still fast and everything here is a prototype.

Just call it on our script: upgrade("hungarian_blog.csv")

and wait a minute and see a lot of improvements...

The new score is ~84764.77 which currently is rank 22 of 200.

With my changes to the hungarian method I achieved rank 10 yesterday which is rank 18 now but with this you're close ;)

Hope you enjoyed reading it and have fun participating.

Oh and what is the new family distribution?

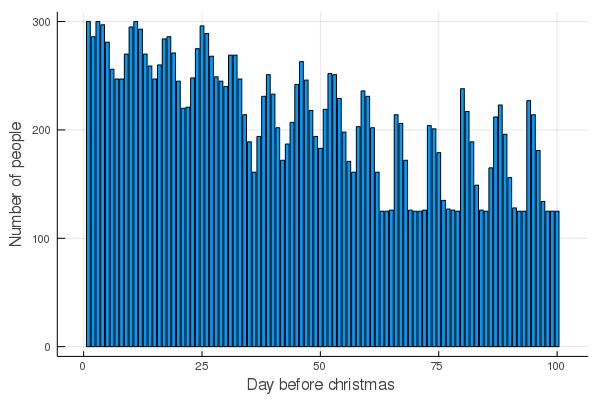
New distribution

As mentioned the day before christmas is crowded and you can see the preference of weekends here ;)

What's next?

I normally write about constraint programming at the moment which you can check out here and currently trying to make it a JuMP.jl solver but have some difficulties.

New ideas for the Kaggle challenge:

Stay tuned ;)

New post is out: Improving and using MIP

And as always:

Thanks for reading and special thanks to my four patrons!

List of patrons paying more than 2$ per month:

Currently I get 9$ per Month using Patreon and PayPal when I reach my next goal of 50$ per month I'll create a faster blog which will also have a better layout:

If you have ideas => Please contact me!

If you want to support me and this blog please consider a donation via Patreon or via GitHub to keep this project running.

For a donation of a single dollar per month you get early access to the posts. Try it out for the last two weeks of October for free and if you don't enjoy it just cancel your subscription.

If you have any questions, comments or improvements on the way I code or write please comment here and or write me a mail o.kroeger@opensourc.es and for code feel free to open a PR on GitHub ConstraintSolver.jl

I'll keep you updated on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de



Want to be updated? Consider subscribing on Patreon for free
Subscribe to RSS
© Ole Kröger. Last modified: June 08, 2020. Website built with Franklin.jl.