Indicator constraint + Benchmarks

Are you new to this series? You might want to check out the start of the series: Creating a constraint solver from scratch

I know it's a lot to read so you might want to just check out the solver itself ConstraintSolver.jl

This was my next up from last time and it feels like I should actually follow my plans one day...

• How about those unit tests?

• Being able to hot start

  • So provide a partial solution to find a feasible solution faster

  • If the partial solution is wrong or optimality should be reached then backtrack all the way back

• Oh yeah I need to decide on the logo. Please help! Logo issue

At least I did some of it. I talked about the logo in the last post: Housekeeping May 2020

Unit tests

I actually added some unit tests and got some nice improvements out of it. If you want to get details check out PR #162

It includes several bug fixes non feature to feature conversions:

• To feature conversion:

  • in equal constraint, if the synching the equal constraint fails

    • I forgot to return false if that happens :/

  • In the less than constraint I computed a worse safe_threshold such that a bit more pruning is possible

• Feature: Better pruning of eq_sum when changing some variables it is reasonable to test the other ones again

One can hopefully see some of the changes in the benchmark section below ;)

Indicator constraint

Before we go to the benchmark section I also want to introduce a new constraint type which doesn't have a benchmark test yet so if you have some ideas: Reach out :)

This constraint is partially supported in PR #167. Will be available in v0.1.8 hopefully soon.

JuMP supports the following syntax for indicator constraints:

@constraint(m, b => {x + y >= 0})

Where the constraint in {} has to be an affine constraint at the moment which means that I don't support an inner alldifferent or table constraint just yet but working on it.

Okay what does that constraint mean?

b is a binary variable and if b = 1 then the constraint must be satisfied otherwise that constraint is not relevant.

The implementation is relatively straightforward I would say and probably gives another good example of how to add a constraint to the solver.

We start with adding a new type in src/types.jl:

mutable struct IndicatorConstraint <: Constraint
    std::ConstraintInternals
    activate_on::MOI.ActivationCondition
    inner_constraint::Constraint
end

We of course need std::ConstraintInternals as in all other constraints to save the indices it uses for pruning and the id of the constraint and other useful information.

The activation_on field is of type: MOI.ActivationCondition and holds information on whether we have b => or !b => so whether we activate the inner constraint on a positive or a negative value.

help?> MOI.ActivationCondition
  ActivationCondition

  Activation condition for an indicator constraint. The enum value is used as first type parameter of IndicatorSet{A,S}.

As you can see it's an @enum which we haven't discussed here before. You might want to check it out yourself in the REPL ;) It's not important for this use case but you might want to be aware that it exists.

Then whenever we create a new constraint type which is different from the x in Set notation we either have to extend JuMP and MOI or maybe they have implemented it already. In ths case we are lucky as it exists already and probably gives us a good stepping stone for implementing the reified constraint which is on my issue list.

Okay let's check the documentation for the indicator constraint.

• JuMP.jl - Indicator

  • doesn't give that much information for implementing it as it's more the user interface side of view

• MathOptInterface.jl - Indicator

For a constraint like y = 1 => {x1 + x2 <= 9} we get:

f = MOI.VectorAffineFunction(
    [MOI.VectorAffineTerm(1, MOI.ScalarAffineTerm(1.0, y)),
     MOI.VectorAffineTerm(2, MOI.ScalarAffineTerm(1.0, x1)),
     MOI.VectorAffineTerm(2, MOI.ScalarAffineTerm(1.0, x2)),
    ],
    [0.0, 0.0],
)

indicator_set = MOI.IndicatorSet{MOI.ACTIVATE_ON_ONE}(MOI.LessThan(9.0))

MOI.add_constraint(model, f, indicator_set)

Which means we need to create two functions in src/MOI_wrapper/constraints.jl:

function MOI.supports_constraint(
    ::Optimizer,
    func::Type{VAF{T}},
    set::Type{IS},
) where {A, T<:Real, ASS<:MOI.AbstractScalarSet, IS<:MOI.IndicatorSet{A, ASS}}
    return A == MOI.ACTIVATE_ON_ONE || A == MOI.ACTIVATE_ON_ZERO
end

this is the function which gets called to check whether the solver supports the constraint. If it doesn't it might call some bridges to support that constraint in a different way. For example I don't directly support the >= (MOI.GreaterThan) constraint but the <= (MOI.LessThan) constraint which can be used when multiplying everything by -1.

Here I support every type of AbstractScalarSet constraint as the inner constraint which means !=, ==, >= and <=. As MOI.ActivationCondition is an @enum I think that I can't dispatch on it at least I wasn't able to. If there is a way please let me know. I just check whether it's an activation condition in the function this time.

The next thing to implement is the MOI.add_constraint function:

function MOI.add_constraint(
    model::Optimizer,
    func::VAF{T},
    set::IS,
) where {A, T<:Real,ASS<:MOI.AbstractScalarSet, IS<:MOI.IndicatorSet{A, ASS}}

That function needs to add the constraint to the model. Therefore several steps need to be performed:

Create the internals constraint part which includes indices the func and the set:

internals = ConstraintInternals(
    length(com.constraints) + 1,
    func,
    MOI.IndicatorSet{A}(inner_set),
    indices
)

here the inner_set is defined by the inner constraint which includes some more lines of code but normally the third parameter is just the set. This is of course only if you want to add a constraint to my solver and not implement such an interface for your own solver for example. There you only need the supports function and this add function with your solver specific code.

My function always ends with:

con = IndicatorConstraint(internals, A, lc)

push!(com.constraints, con)
for (i, ind) in enumerate(con.std.indices)
    push!(com.subscription[ind], con.std.idx)
end

well the first line depends on the constraint type you use ;)

The last lines just add the constraint to the model and fills the subscription field which decides later which function gets called when a specific variable changes.

MOI also wants a special return statement:

return MOI.ConstraintIndex{VAF{T},MOI.IndicatorSet{A, ASS}}(length(com.constraints))

It must include the func and set type as well as the id of the new constraint.

Some of you might know already that there are at least four more functions to implement:

• in src/hashes.jl

  • constraint_hash

• in src/constraints/NAME_OF_CONSTRAINT.jl

  • prune_constraint!

  • still_feasible

  • is_solved_constraint

I don't think that the implementation of the indicator constraint is that interesting. Basically just check whether the binary variable is active based on the MOI.ActivationCondition and then call the functions of the inner_constraint.

You can check all the code in my PR #167

In the next post I'll hopefully explain how to extend JuMP in a way to also support constraints like b => {[x,y] in CS.AllDifferentSet()} Currently I'm a bit stuck on that one but hopefully figure it out next week.

Updated Benchmarks

I really need a tool to do them automatically... Currently I run them by hand and have to copy the results to visualize them. It's a bit of a pain but gladly I do automatic benchmark tests on every pr now it just isn't a beautiful graph :D

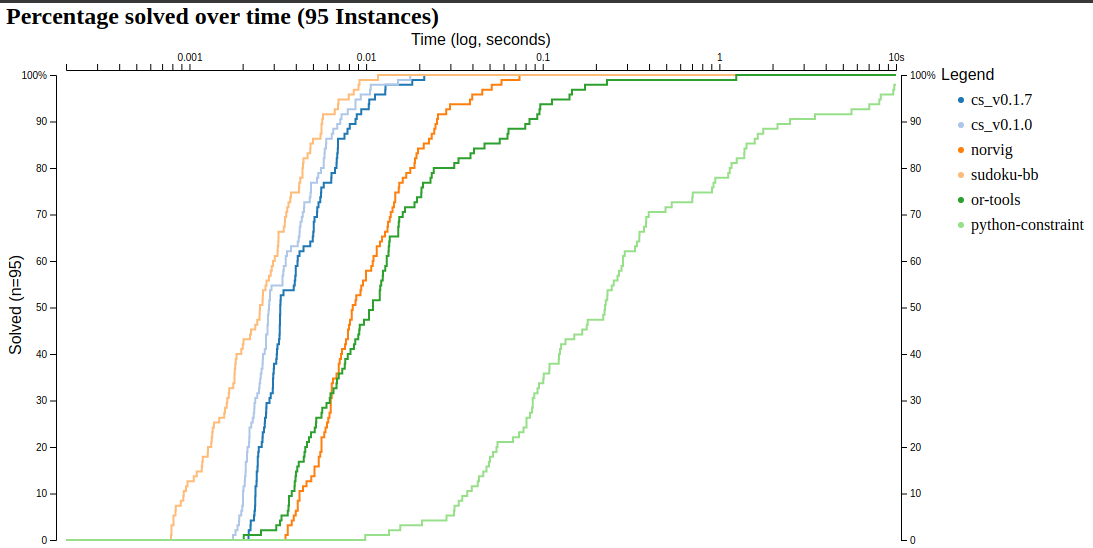
Well yeah it got a bit slower in the new versions but the instances are solved so fast that it's hard to get whether it's significant. I should have better benchmarks for the alldifferent constraint but I also have the killer sudoku one which uses the alldifferent and the == constraint.

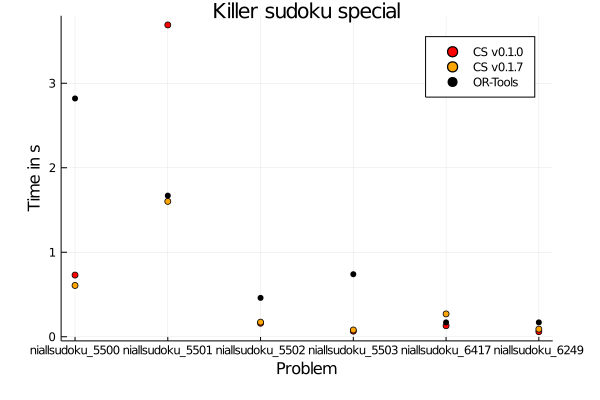
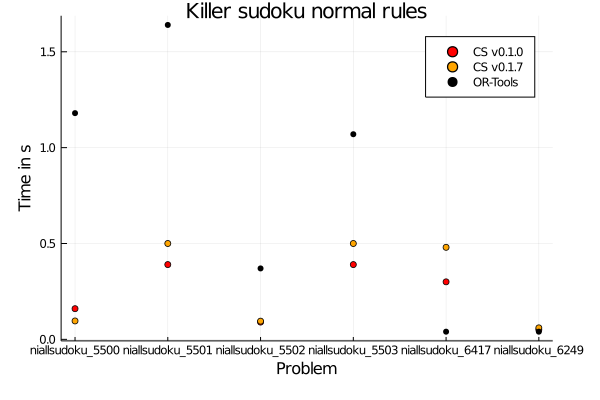
As a reminder the special rules are the ones where the cage does not have an alldifferent constraint. In that case there is some nice improvement for the 5501 problem.

Besides that there is neither big improvement not recession so I'm quite happy with the results. In general there is only one instance where OR-Tools is significantly faster but you know that this is just a rough comparison anyway as the instances are small and maybe I focus on solving such neat puzzles but OR-Tools definitely tries to catch the big fishes ;)

Thanks everyone for reading and maybe check out my new streaming adventure on Wednesday 5 PM UTC on Twitch

Next post is done: Indicator Part 2

Thanks for reading and special thanks to my six patrons!

List of patrons paying more than 4$ per month:

• Site Wang

• Gurvesh Sanghera

• Szymon Bęczkowski

Currently I get 19$ per Month using Patreon and PayPal.

For a donation of a single dollar per month you get early access to the posts. Try it out at the start of a month and if you don't enjoy it just cancel your subscription before pay day (end of month).

Any questions, comments or improvements? Please comment here and/or write me an e-mail o.kroeger@opensourc.es and for code feel free to open a PR/issue on GitHub ConstraintSolver.jl

I'll keep you updated on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de

Want to be updated? Consider subscribing on Patreon for free