Constraint Solver: Priority Queue
Creation date: 2020-12-11
As Javis has now a decent version v0.3, I returned back to work on my ConstraintSolver in the last couple of weeks.
The constraint solver is a over a year old project which I try to document on this blog. If you missed the start of this series please have a look here.
All other posts of the series can be found via the sidebar.
A bit housekeeping
In the last post I made an improvement for combining != constraints for better bound computation. There were some drawbacks with that especially that the resulting all_different constraint is much slower than the != constraint and is only useful for strong dependencies of the variables as given in Sudoku examples.
I've implemented an own version of strongly connected components to reduce the memory consumption of general all different constraints but that wasn't as helpful as I thought. It still reduces memory though so that is part of v0.4.1.
Why a Priority Queue?
Sometimes I do some profiling on certain instances to check what the slowest part for that instance was and try to improve that. This time I profiled a killer sudoku. (I covered this in the equality constraint posts)
The killer sudoku was quite hard such that a lot of nodes (~50,000) needed to be explored. The pruning was relatively fast in these cases and it turned out that finding the next node to explore took an unreasonable amount of time (~50% of the running time).
This was part of the code for depth first search before:
node_idx = 0
best_fac_bound = typemax(Int)
best_depth = 0
for i = 1:length(backtrack_vec)
bo = backtrack_vec[i]
if bo.status == :Open
if bo.depth > best_depth || (
obj_factor * bo.best_bound < best_fac_bound &&
bo.depth == best_depth
)
node_idx = i
best_depth = bo.depth
best_fac_bound = obj_factor * bo.best_bound
end
end
endI'm not sure whether I have to explain why this is bad but let's do it anyway 😄
First of all, it goes through all nodes and checks whether they are open. If open it takes the node with the highest depth and if two nodes have the same depth it compares the best bound.
obj_factor is 1 or -1 and depends on whether it's a minimization problem or a maximization one.The first thing that is bad about this is that we iterate over closed nodes as well which are often much more than the open ones. It's a simple == :Open check but still.
Afterwards it's still always a \(\mathcal{O}(n)\) operation where \(n\) is the number of open nodes.
How can this be solved?
Exactly by using a priority queue which stores the depth, index of the node as well as the best bound for all open nodes.
What is a Priority Queue?
A priority queue is a data structure which can be used for the above described problem. It normally has the following functions:
insert a new element with a given priority
change the priority of an element
get the element with lowest priority
remove the element with lowest priority
The running times of these can depend on the implementation. It normally uses a tree or a forest structure where the smallest priority is at the top such that getting it is a simple \(\mathcal{O}(1)\) computation. Insert can sometimes be done in constant time if it's a forest structure or in \(\mathcal{O}(log(n))\) at maximum. Change and remove are similar.
The most basic implementation is using a so called heap where each node has at most two children and the children have a bigger priority.
Changing the priority can have two effects either we have to go up in the tree or go down but the depth of the tree is \(\log_2(n)\) such that we get our running time.
Removing the element with lowest priority can be done similar to changing the priority and have it as a leaf node where it can easily be removed.
If you want to check out different ways have a look at:
For the constraint solver we do one insert, one update for bound computation and a maximum of one delete per node.
Our running time for all of them is in \(\mathcal{O}(log(n))\) which is an improvement to before and our \(n\) is now actually the number of open nodes and not of all nodes.
Implementation
I know that I do a lot of implementations from scratch but often it's taking quite some time and it's obviously not always faster 😄. In this case I was happy enough to understand how it works as I had it in university a couple of years ago and actually currently teach it to some students. 😉
Therefore I decided to use DataStructures.jl for this one and I really enjoyed working with it.
I guess in some languages I would have to think about how I represent the priority as a number as a normal priority queue works with simple numbers.
For my use case it's important, that I look for the highest depth first, then check for the bound and do tiebreaks with the unique id of the backtrack node.
BTW for best first search I would check the bound first, then the depth and then the unique id.
The priority queue is only interested in whether an element is smaller than another such that I can easily define a struct and define the isless function and everything works as it should.
abstract type Priority end
struct PriorityDFS{T<:Real} <: Priority
depth::Int
bound::T
neg_idx::Int # the negative backtrack index (negative because of maximizing)
end
function Base.isless(p1::PriorityDFS, p2::PriorityDFS)
if p1.depth < p2.depth
return true
elseif p1.depth == p2.depth
if p1.bound < p2.bound
return true
elseif p1.bound == p2.bound
return p1.neg_idx < p2.neg_idx
else
return false
end
end
return false
endI actually decided to use a maximizing priority queue as it seems more natural to me. I've implemented the same thing for PriorityBFS.
The above get_next_node function from before is reduced to:
backtrack_idx, _ = peek(com.backtrack_pq)Additionally, When I close the node I have to remove it from the queue and update the best bound when I compute it.
Special case
Besides DFS and BFS the ConstraintSolver package also implements DBFS which means depth first search until a solution is found and then do best first search. In this case I delete the priority queue and rebuild the new one from scratch but this needs to be done at most once so the running time isn't really important.
Benchmark
It's always good to benchmark whether it worked. Here I've run it on a couple of eternity II puzzles.
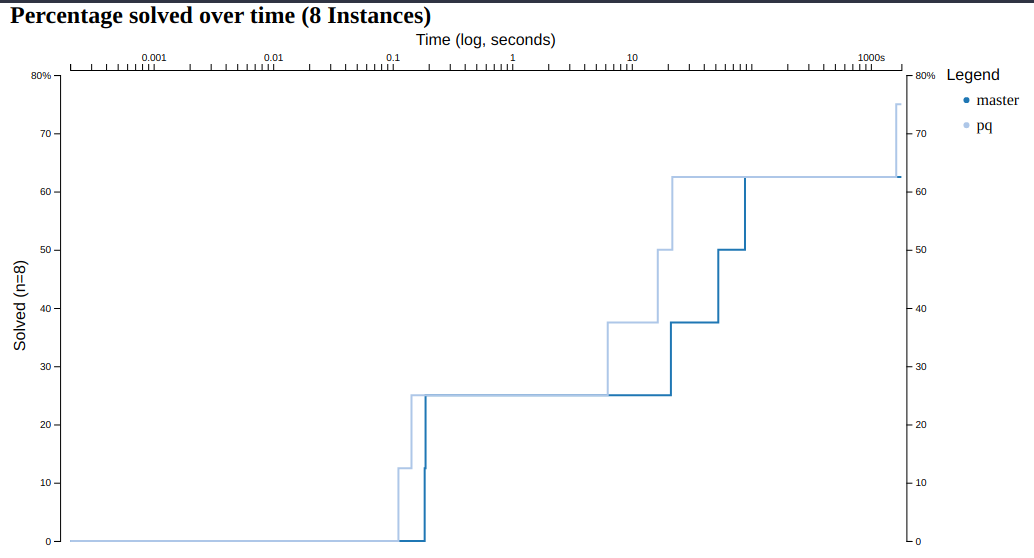
One can see that the solver can solve one more puzzle now in the time limit of half an hour and can solve some of them five times faster than before.
Future of the ConstraintSolver
Currently I'm working on the solver almost daily besides my master thesis. A user of the solver is so kind to test it out with different problems and opened a couple of wishlist issues and helped to find some stuff that wasn't working.
Therefore, a new version is coming out relatively often now. The next post in this long long series will be about sorting a list of integers by using a new constraint type.
Yes that new constraint is also great for more reasonable things but sorting is nice as well. One can write a faster sorting algorithm in a handful of lines but this one is special 😉
Anyway, stay tuned!
Thanks everyone for checking out my blog!
Special thanks to my 10 patrons!
Special special thanks to my >4$ patrons. The ones I thought couldn't be found 😄
Site Wang
Gurvesh Sanghera
Szymon Bęczkowski
DShiu
For a donation of a single dollar per month you get early access to these posts. Your support will increase the time I can spend on working on this blog.
There is also a special tier if you want to get some help for your own project. You can checkout my mentoring post if you're interested in that and feel free to write me an E-mail if you have questions: o.kroeger <at> opensourc.es
I'll keep you updated on Twitter OpenSourcES.
Want to be updated? Consider subscribing on Patreon for free


