Constraint Solver Part 3: More Pruning and Benchmarking

Series: Constraint Solver in Julia:

• Part One: Setup and backtracking

• Part Two: Pruning

This is part 3 of the series about: How to build a Constraint Programming solver?

In this part we want to make a minor but important update to the old post as I missed something as well as doing some bechmarking with other constraint programming solvers or specialized sudoku solvers.

Let's have a look at the video from the last post:

Explanation:

Last time we have set a value while backtracking and then removed values from the search space and maybe set new values due to fixing this single value.

• black: Given values

• blue:

  • beginning: pruned before backtracking

  • later: set or pruned during backtracking (might be wrong)

• green cell: last set by backtracking

• orange cell: pruned by green cell (or later other orange cells)

At that moment I didn't completely think that through and only when I had a look at the visualization I made I realized that it's a bit stupid not to further propagate the new changes as well.

That is the only change on the code basis for this post and after that I'll show you some benchmarking results which will not be that awesome yet as it's more like a spoiler and preparation for the next post which will be longer.

So after the first pruning in our backtrack function: GitHub Line

we add a part to prune further on the fixed values:

# prune on fixed vals
co_idx = 1
constraint_idxs_dict = Dict{Int, Bool}()
# get all constraints which need to be called (only once)
while co_idx < length(constraint_outputs)
    constraint_output = constraint_outputs[co_idx]
    for fixed_ind in keys(constraint_output.fixed)
        inner_constraints = com.constraints[com.subscription[fixed_ind]]
        for constraint in inner_constraints
            constraint_idxs_dict[constraint.idx] = true
        end
    end
    co_idx += 1
end
constraint_idxs = collect(keys(constraint_idxs_dict))

There we just check which constraints need to be called again and the in a while loop we call the constraints and add constraints to our list if some cell got fixed:

con_counter = 0
# while we haven't called every constraint
while length(constraint_idxs_dict) > 0
    con_counter += 1
    constraint = com.constraints[constraint_idxs[con_counter]]
    delete!(constraint_idxs_dict, constraint.idx)

    constraint_output = constraint.fct(com, constraint.indices; logs = false)
    push!(constraint_outputs, constraint_output)
    push!(constraints, constraint)
    if !constraint_output.feasible
        feasible = false
        break
    end

    # if we fixed another value => add the corresponding constraint to the list
    # iff the constraint will not be called anyway in the list 
    for ind in keys(constraint_output.idx_changed)
        for constraint in com.constraints[com.subscription[ind]]
            if !haskey(constraint_idxs_dict, constraint.idx)
                constraint_idxs_dict[constraint.idx] = true
                push!(constraint_idxs, constraint.idx)
            end
        end
    end
end

Now you might say that looks awful why is that so much code and it seems like we did that already. You know what, you're damn right. Therefore the code gets it's own function prune!(com, constraints, constraint_outputs) and returns feasible, constraints, constraint_outputs and it will also be called in our main solve function directly after calling every constraint function ones.

Additionally I found that we always backtrack from left to right and then pruning isn't working that well in Sudoku because all the surrounding cells are already fixed.

Therefore my idea was to choose the cell with the least amount of possibilities as before but if there are several choices take the one where the number of possibilities in related cells is the highest as I assume that we can prune more in that case.

It's just some for loops so not that interesting I think.

You can see the corresponding video visualization:

You can see that this is much faster and way less backtracking is needed.

I also marked the cell now which made a current configuration infeasible.

In this particular case we get:

Info: 
com.info = pre_backtrack_calls = 30
backtracked = true
backtrack_counter = 7

We removed the backtrack counter from 54 to 7.

Let's have a short look at the timing:

julia> @benchmark main(;benchmark=true)
BenchmarkTools.Trial: 
  memory estimate:  1.28 MiB
  allocs estimate:  26235
  --------------
  minimum time:     1.267 ms (0.00% GC)
  median time:      1.450 ms (0.00% GC)
  mean time:        1.886 ms (14.97% GC)
  maximum time:     68.694 ms (97.87% GC)
  --------------
  samples:          2641
  evals/sample:     1

That is another nearly 3X improvement compared to the last version.

Benchmarking

Before you're getting too exited about this let's have a look at some other solvers ;)

I compared my solver to python-constraint by using an implemention I found on GitHub . It is a Constraint Solver in Python and I compared it to a famous (well in this area) sudoku solver written by Peter Norvig which he described in his blog: Solving Every Sudoku Puzzle

Maybe I'll try to add MiniCP and MiniZinc to it but never used them...

Please post some other solvers I should compare against in the comments. I'll add them in the next blog post ;)

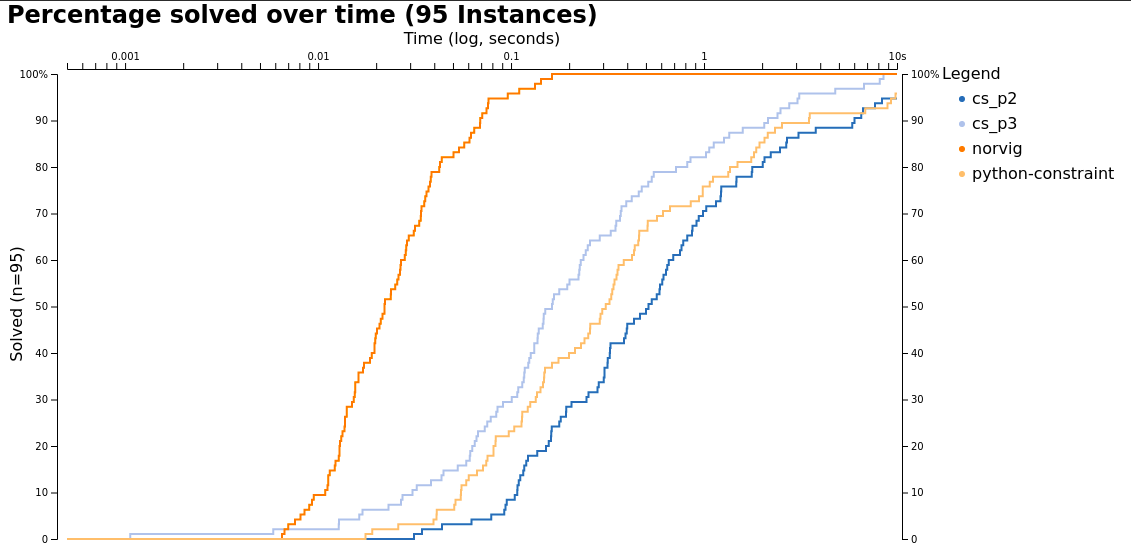
The 95 sudokus are from a list Norvig mentioned in his blog as well Top 95 sudokus

For each program I only measured the solve call. I've benchmarked this version of the blog cs_p3 as well as the previous version from Part 2 cs_p2.

You can clearly see that the solver by norvig is the fastest by quite a bit (about 50x faster than our current version) log plot!.

In the next blog I'm trying to change that. I'm not done yet but I think it will be quite comparable. (Additionally if you have some hard sudokus => comment)

I've tried also the Part 1 version of this series but it was too disappointing :D (well I didn't want to wait for too long)

As you can see the current version is able to solve the sudokus faster than python-constraint which it didn't in the previous version.

I might publish a website for this benchmarks later similar to the one I created for my MINLP solver Juniper.jl. The performance of that is available here.

For the next post you might want to think about yourself how we could prune more values. Maybe the visualization on YouTube helps or just try to solve a sudoku by hand again. It might be your last time ;)

Next post is out about a better implementation of the alldifferent constraint

And as always:

Thanks for reading!

If you have any questions, comments or improvements on the way I code or write please comment here and or write me a mail o.kroeger@opensourc.es and for code feel free to open a PR on GitHub ConstraintSolver.jl

Additionally if you want to practice code reviews or something like that I would be more than happy to send you what I have before I publish. ;)

I'll keep you updated if there are any news on this on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de

If you enjoy the blog in general please consider a donation via Patreon to keep this project running.

Want to be updated? Consider subscribing and receiving a mail whenever a new post comes out.

Enter your email

Powered by Buttondown.