ConstraintSolver.jl v0.1.0
Creation date: 2020-04-06
I confess that while I'm writing this it isn't actually a package yet and I plan to publish this post to my Patrons today. One day before it will be a release (if nobody has any problem with it :D).
Edit: (7th of April) It now is an official package :) You can install it with:
] add ConstraintSolverHaven't posted here for quite a while as I worked on the Covid19 visualization and did some other stuff during quarantine time. Had a look back into what I promised to write about and feel more and more the urge to use a new blog to have a better structure and a search function. Hopefully there will be a first working version in the next months. I already have one version with a very limited number of posts for my Patrons and writing new posts there first and transfer them over to the old one.
Anyway I found that I wanted to talk a bit about the general structure again using Multiple Dispatch. It is a talk about multiple dispatch in Julia. I more and more enjoy that feature. Well this post is not about multiple dispatch though but you should definitely watch the talk. I think post 20 (so the next one) will be about the general structure again which includes some dispatch things.
What the hell is this post about then?
Oh okay sorry I drifted away... There were some issues/missing features I had before I wanted to release this basic version 0.1.0.
I'll go through them one by one here and we'll see how long this post will be.
All solutions
I think I haven't written about getting all solutions yet. I mentioned it at least three times before that this will be interesting for sudoku. Checking whether every sudoku has exactly one solution is also a nice feature if you want to create a sudoku puzzle yourself.
There are several options to implement this in the backend but the frontend side is what might be more interesting to you. In the backend I simply have a vector of vectors which saves every solution and I deactivate the early breaks in the backtrack functions to actually fully search the tree.
I have two options: all_solutions and all_optimal_solutions which are the same for feasibility problems and for optimization problems you might be only interested in optimal solutions but for small problems it might be nice to get all feasible solutions.
For the frontend you need to implement:
function MOI.get(model::Optimizer, ::MOI.ResultCount)
return length(model.inner.solutions)
endsuch that the user can query the number of solutions with: MOI.get(m, MOI.ResultCount()) when m is the model. Additionally to get the actual solutions one needs to change the backend of the JuMP.value function slightly with:
function MOI.get(model::Optimizer, vp::MOI.VariablePrimal, vi::MOI.VariableIndex)
check_inbounds(model, vi)
return model.inner.solutions[vp.N].values[vi.value]
endwhere the second argument defined the solution number N you're interested in. The user can get the value of x in the second solution with: JuMP.value(x, result = 2) then.
The same for the objective value:
function MOI.get(model::Optimizer, ov::MOI.ObjectiveValue)
return model.inner.solutions[ov.result_index].incumbent
endFor the user: JuMP.objective_value(m, result = 2).
Branch splitting strategies
Maybe you remember the first strategy I used for solving sudokus and killer sudokus. This is probably one reason why one shouldn't specify the problem that early and define the constraint solver around it. On the flip side it will be boring to write about it without examples.
When we couldn't prune anymore we had to choose a new variable to branch on and split it into N nodes. N is the number of possible values. Which was always at most 9 for both of those problems. Then I used different optimization problems for tests which I haven't written about it here yet as well as some simple problems with a bigger N like 100. Where the constraints don't make it that simple at first to prune anything.
i.e
1 <= x,y <= 100
x+y == 125
min. xYou can't prune anything and it's not a good problem for constraint solvers anyway but it shouldn't be too hard to solve. Nevertheless it's a waste of time to split x into 100 possible child nodes.
Therefore I chose to always have two children in my tree and just split it into two nodes of approximately the same size.
In the above example I would have x <= 50 as one node and x >= 50 on the other side. In the next step I would chose the former because it has the smaller x and split it again into two parts.
This is faster even though there a better ways to handle this by using the relaxation of the problem but I wanted to have it in constraint solver style without too much bound computing at the moment.
Unfortunately this is not a really good approach for sudoku and killer sudoku. There fixing a value is much more reasonable. One approach would be to check which constraints are present, how many values we have etc to decide this.
I researched a bit what others use and found that they normally split it into two parts but some different then what I do namely if we have x = 1..100 we split it into x=1 and x != 1 or x=100 and x != 100.
Which isn't perfect but somewhat a reasonable compromise I think.
The user has the option to chose between :Smallest, :Biggest and the previous way :InHalf now with the option branch_split.
I think it might be interesting to how to implement this with multiple dispatch.
Have four methods:
function get_split_pvals(com, ::Val{:Smallest}, var::Variable)
function get_split_pvals(com, ::Val{:Biggest}, var::Variable)
function get_split_pvals(com, ::Val{:InHalf}, var::Variable)
function get_split_pvals(com, ::Val{:Auto}, var::Variable)Normally I would have written four functions:
function get_split_pvals_smallest(com, var::Variable)
function get_split_pvals_biggest(com, var::Variable)
function get_split_pvals_inhalf(com, var::Variable)
function get_split_pvals_auto(com, var::Variable)or something like that. Then when calling I would have:
if option == :Auto
get_split_pvals_auto(...)
elseif option == :Smallest
get_split_pvals_smallest(...)
elsif ...which means that you need an extra elseif whenever you come up with a new option.
In Julia you can use the above version and the user defines the option with "branch_split" => :Smallest then you define: branch_split = Val(option.branch_split) internally and you can just dispatch on the option.
Logging
Actually the above change of splitting somehow destroyed some killer sudokus but I figured that this must have other more severe reasons. I started with some logging a while ago but haven't used it since then because the front end was not that nice. It's not really good now but it's getting better and I hope I can also publish that in the near future. Maybe some people out there have a better understanding of css than me (I'm sure because mine is very poor). Additionally I'm more on the practical side than the visual appealing one so please help me out then. The current version looks like this:
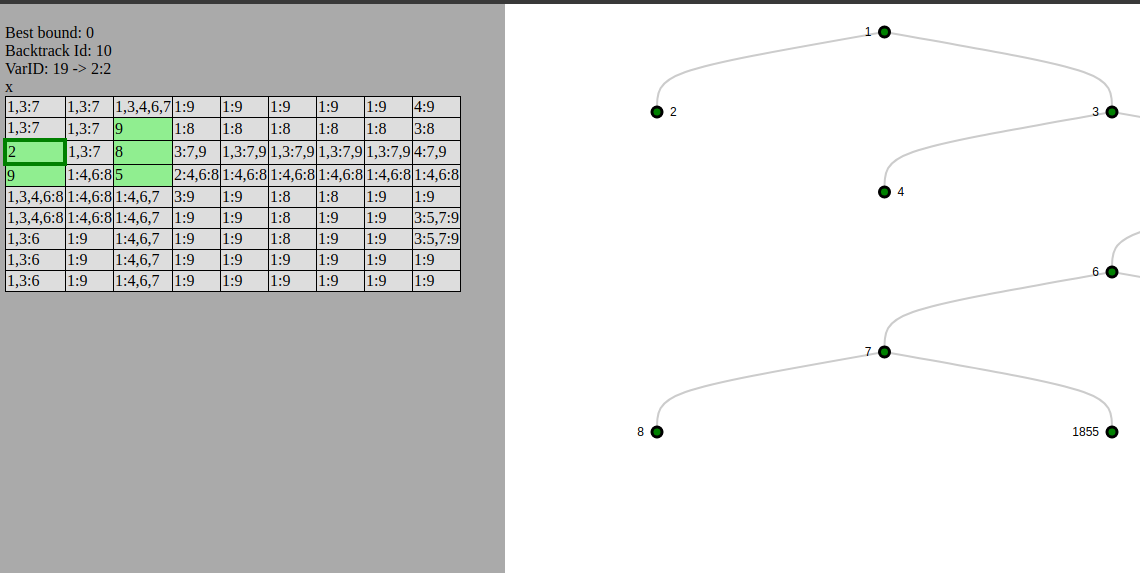
On the left hand side you can see the killer sudoku search space. The light green cells are fixed and the one with the dark green border is the current branching variable. It's not possible to see the constraints here but I think it's quite helpful nonetheless.
The corresponding killer sudoku:
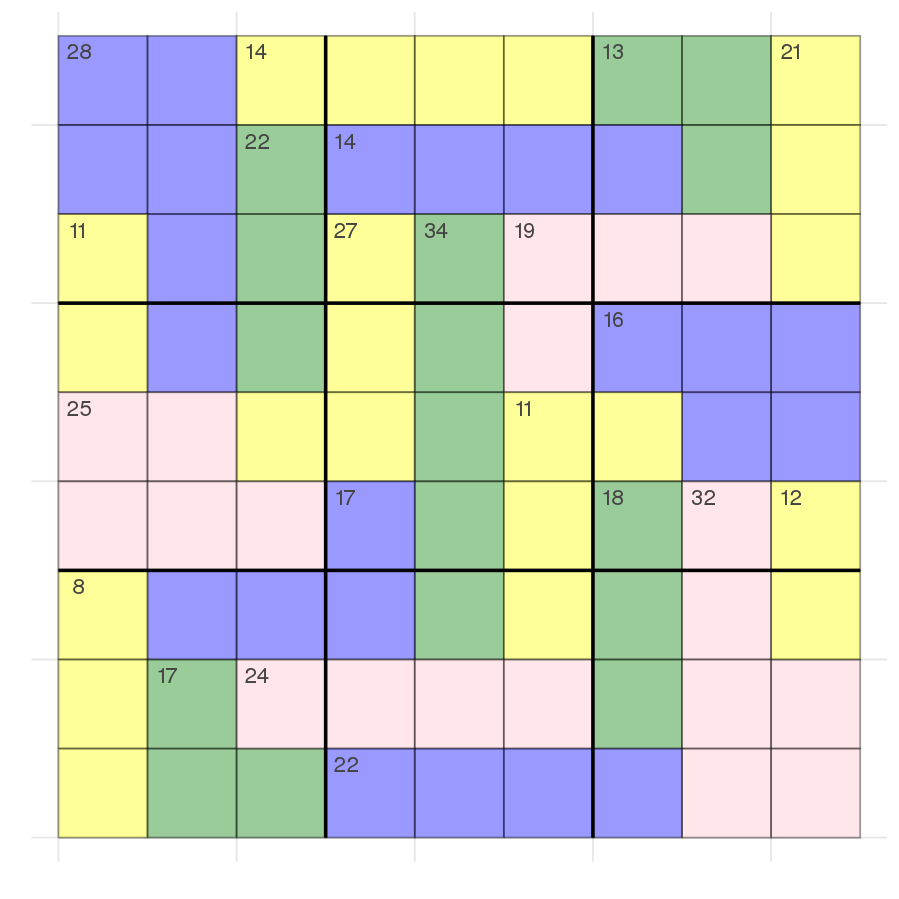
Now you can see that there are still a lot of variables which can take all values 1 to 9. Additionally there are some constraints which could limit the search space even further.
One example: In the bottom left we have three cells which should sum up to 8 and because they are in the same 3x3 box and same column they also need to be all different. This should limit each cell to the value 5 and not 6.
I decided to not fix this as normally constraints are not meant to communicate with each other which I already break for simple ones with only two cells instead of three. The sum constraint in general is meant to be fast and not exhaustive. There is often more to prune but that would make it a slower algorithm.
Nevertheless the one problem I wanted to tackle is the addition of extra constraints which are implicit. This can be of course done by the user but I think it's not wrong to let the solver do something like this as well.
There should be an output for it to see if constraints were added and an option to disallow that.
It was very slow to solve this problem so I had a go for myself. Trying to prune a bit in my head and check whether my mind can easily prune more than the solver without using exhaustive search. The middle column with the five green cells with a sum of 34 can be used to add an additional constraint when knowing that the column is an all different constraint with numbers 1-9. This means that every digit needs to be used exactly once which implies a sum of 45 (sum(1:9)). Which means that the four values in that column which are not part of the sum = 34 constraint need to add up to 11. Even without using the alldifferent part there it means that there is no 9 possible in any of those cells because 9+1+1+1 = 12.
I've added this into my simplify function which needs a rewrite as well. That function actually generates new constraints based on old once so I think even the name is wrong :D
How to register the package?
I think that are the main things I have changed since last time. In this last section I want to talk a bit about how registering a package works.
There is a package for that :D Registrator
If you followed this series from the beginning... Well first of all I'm proud ;) ... you have seen how to create a module/package which basically means that you are already ready to register it. Btw: I've explained this in my first post.
Then you can create an issue in your repository with the comment:
@JuliaRegistrator register()which you can see here in action.
Which triggers a PR at JuliaRegistries/General.
There tests are run including one which I always forget... It tests whether all your dependencies have an upper bound. Therefore mine failed and then I added them in my Project.toml:
[compat]
Formatting = "^0.4.1"
JSON = "~0.18, ~0.19, ~0.20, ~0.21"
JuMP = "^0.21.0"
MathOptInterface = "^0.9.1"
MatrixNetworks = "^1"
julia = "1"That format is explained here.
Additionally I've also added CompatHelper which opens a PR when a dependency has a new version which is currently not supported by your package. The tests for the PR will check then whether it still works or whether you have to fix something. Another helpful one is TagBot which creates a GitHub release whenever a new version got released and shows the closed issues and pull requests.
Try it out!
If you are interested in this project please try it out. I'm sure there are still some bugs non-features. Would be awesome if you can create issues if there is something unclear, slow, wrong, etc...
I think it will be easier to develop it further this way and for you it should be quite simple to install it now:
] add ConstraintSolver and if there are is a new release just run ] update instead of pulling the master of my repo over and over.
Thanks for your support! I'm also happy to announce that my abstract for this project got accepted for JuMP-dev 2020 which means that I have to develop it further to be able to show something nice in mid June ;)
Let's hope that by then everything is a bit more normal in the world otherwise it will probably be an online event.
Thanks for reading and special thanks to my five patrons!
List of patrons paying more than 4$ per month:
Site Wang
Gurvesh Sanghera
Szymon Bęczkowski
Currently I get 18$ per Month using Patreon and PayPal.
For a donation of a single dollar per month you get early access to the posts. Try it out at the start of a month and if you don't enjoy it just cancel your subscription before pay day (end of month).
Any questions, comments or improvements? Please comment here and/or write me an e-mail o.kroeger@opensourc.es and for code feel free to open a PR/issue on GitHub ConstraintSolver.jl
I'll keep you updated on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de
Want to be updated? Consider subscribing on Patreon for free


