Building an Enigma emulator and a Bombe

Creation date: 2020-02-09

I got a bit distracted on my work of building a constraint solver which is a series of 17 posts now. Check it out if you're interested in solving sudokus, graph coloring, JuMP or well generally contraint solving. This time I want to show you what I've done the last couple of days.

YouTube suggested me this video from Code Bullet about building an Enigma Machine. It was somehow on my imaginary list of things I wanted to code like a sudoku solver some years ago.

Additionally I want to code a chess computer but that's something for another day.

Alright let's start with the Enigma. First of all I will shortly explain what it is about then I'll start with creating the Enigma package in Julia with starting which functions we need to encrypt and decrypt messages.

In the second part you can read more about the flaws of the Enigma machine and how they can be used to crack the code so decrypt messages without knowing the setting.

If you enjoy videos more you can also check out the video I made about this topic:

A bit of a story

The Enigma was used in the World War II by the Germans to have a secure communication in their military. They thought that their machine is sooo good that it is unbreakable. Well they weren't the first to think that about a new cryptographic technique and probably not the last. The code was famously cracked by Alan Turing and others at Bletchley Park during the war. Which means that they were able to save a lot of lives and end the war earlier.

Maybe you have seen the movie The Imitation Game with Benedict Cumberbatch about that story. Even though it is simplified as always it is a good movie.

Because we dive into the actual Enigma Machine we might want to have a very short look at previous methods of decrypting and I'm not an expert on this so it's just a short overview of simple methods that I find interesting.

First part of every cryptography section should be the Caesar method where one only replaces a letter with a different letter and even simpler just moving the alphabet by a number of steps like this.

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 
G H I J K L M N O P Q R S T U V W X Y Z A B C D E F

Things that come to mind if cracking such codes are:

Is it safe even if they know the method but not the settings?
How many possibilities are there?

In this case there are only 26 setting and one of them is the plain text so it is obviously not good if you know the method.

What if we just randomly set the letters instead of shifting?

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 
D J W Z A O M N T L X R B S C I U Y Q G P F K H E V

That looks much harder, right? How many possibilities are there? For the first letter we have 26 possibilities then 25 and so on...

\[ 26! = 403291461126605635584000000 \]

That's what I call a massive number. It's about \(10^{26}\). So why don't we use just that?

Can you read: TB DBBF CN ERNNPB PNAB MCBAP MDPMFB NUG GNNAP NG KQHEBP ND NUG FHMQX THX CN TNGZ TRMER TB EHD BHPMQX GBABAIBGHDF TRMER TB EHD HPPNEMHCB CRB CRMDLP TB HMA CN ABANGMJB TMCR MD AX EHPB CRB BQBABDCP NS CRB KBGMNFME CHIQBMCP MAKNGCHDC CN NGFBG CRBA IBEHUPB TB TMQQ DBBF CRB NGFBG CN GBABAIBG CRB NGFBG NS CRB ERBAMEHQ BQBABDCPCRBGB HGB HQTHXP HC QBHPC MCBAP MDPMFB BHER GNNA XNU EHD GBABAIBG XNU AMLRC CRMDZ CRHC CRBGB HGB THX ANGB IUCNZHX MA H LUX TRN FNBP DNC RHOB AUER PCUSS MCP BHPX CN SMDF SNG BHER GNNA PNAB AMLRC RHOB ANGB PNABNDQXSMOBCN GBABAIBG CRB NGFBG MCP BHPMBG CN RHOB BWHECQX CRB PHAB HANUDC NS MCBAP MDPMFB BHER GNNA NG KQHEB MD XNUG EMCXHC CRB BDF NS CRMP BWKBGMABDC M THDC CN IB HIQB CN DHAB CRB ENGGBPKNDFMDL BQBABDC CN BHER NGFMDHQ DUAIBG CN SMDF CRB BQBABDC SNG CRB NGFMDHQ DUAIBG SNG MDPCHDEB M EHD LN CN CRB SMSCBBDCR GNNA HDF QNNZ HC CRB CRMGF MCBACRB GUQB MP CN HFF CN XNUG DUAIBG HDF FMOMFB MC IX CN LBC CRB DUAIBG NS CRB GNNA NG THX HDF CRB GBAHMDFBG TMQQ IB CRB DUAIBG NS CRB MCBA MD CRHC GNNA

It's English text from one of my blog posts and I forgot the shuffled order on how to decrypt it. First of all you might think okay it's bad because I left the spaces in it which means that CN is probably something like We, in,an,on,to etc. We can be at least quite sure that H or M which are single are I and a. We can set that and step by step we might be able to get it. Let's remove the spaces and it gets a bit messier, right?

TBDBBFCNERNNPBPNABMCBAPMDPMFBNUGGNNAPNG KQHEBPNDNUGFHMQXTHXCNTNGZTRMERTBEHDBHPM QXGBABAIBGHDFTRMERTBEHDHPPNEMHCBCRBCRMD LPTBHMACNABANGMJBTMCRMDAXEHPBCRBBQBABDC PNSCRBKBGMNFMECHIQBMCPMAKNGCHDCCNNGFBGC RBAIBEHUPBTBTMQQDBBFCRBNGFBGCNGBABAIBGC RBNGFBGNSCRBERBAMEHQBQBABDCPCRBGBHGBHQT HXPHCQBHPCMCBAPMDPMFBBHERGNNAXNUEHDGBAB AIBGXNUAMLRCCRMDZCRHCCRBGBHGBTHXANGBIUC NZHXMAHLUXTRNFNBPDNCRHOBAUERPCUSSMCPBHP XCNSMDFSNGBHERGNNAPNABAMLRCRHOBANGBPNAB NDQXSMOBCNGBABAIBGCRBNGFBGMCPBHPMBGCNRH OBBWHECQXCRBPHABHANUDCNSMCBAPMDPMFBBHER GNNANGKQHEBMDXNUGEMCXHCCRBBDFNSCRMPBWKB GMABDCMTHDCCNIBHIQBCNDHABCRBENGGBPKNDFM DLBQBABDCCNBHERNGFMDHQDUAIBGCNSMDFCRBBQ BABDCSNGCRBNGFMDHQDUAIBGSNGMDPCHDEBMEHD LNCNCRBSMSCBBDCRGNNAHDFQNNZHCCRBCRMGFMC BACRBGUQBMPCNHFFCNXNUGDUAIBGHDFFMOMFBMC IXCNLBCCRBDUAIBGNSCRBGNNANGTHXHDFCRBGBA HMDFBGTMQQIBCRBDUAIBGNSCRBMCBAMDCRHCGNNA

In the world of cryptography we are now Eve the eavesdropper and just got the message send by Alice to Bob. How can we crack the code? Yeah I know maybe you are just here because of Enigma but I think we should know first on why it was an important machine and why simple codes like these don't work well.

It is just a random thing at the moment actually it just came to my mind to write about it. Which means I'm totally unprepared but I think you'll be able to crack the code with the following method and a bit trial and error.

Let's get some help from Julia

using Plots

secret = "TBDBB...NA"
alphabet = ['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z']

counting = zeros(Int, 26)
for c in secret
  println(c)
  counting[Int(c-64)] += 1
end

bar(alphabet, counting ./ length(secret); label="Frequency",
           xticks = (0.5:1:26, alphabet))

That gives us the letter frequency in our secret text

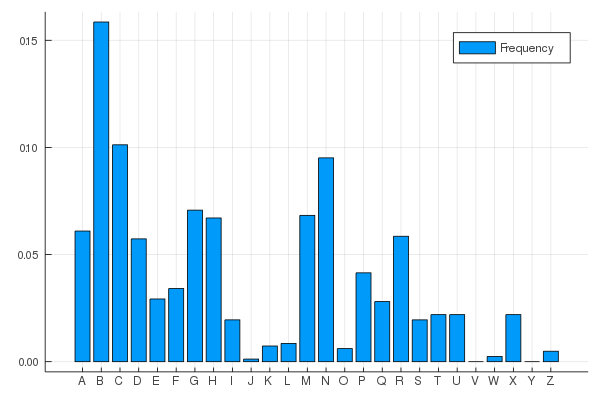
and from Wikipedia we get the letter frequency in a normal english text:

Letter frequency in english text

Source: Wikipedia: Letter frequency

So I would bet that the actual 'E' got encrypted by a 'B' and that the actual 'A' and 'T' are encrypted as 'N' and 'C' or the other way around.

Then you get:

_E_EE_TA__AA_E_A_E_TE_______EA___AA__A_____E_A_A______
____TA_A________E___E______E_E__E__________E______A___
TET_ET______E___TA_E_A___E__T________ET_EE_E_E_T_A_T_E
_E__A___T___E_T____A_T__TTAA__E_T_E__E____E_E_____EE_T
_EA__E_TA_E_E__E_T_EA__E_A_T_E__E_____E_E_E_T_T_E_E__E
_______T_E__T_TE_______EE____AA__A_____E_E__E__A_____T
T____T__TT_E_E__E____A_E__TA___________A_AE__AT___E___
__T____T_E___TA_____A_E____AA__A_E____T___E_A_E_A_EA__
____ETA_E_E__E_T_EA__E__T_E___E_TA___EE___T__T_E___E__
A__TA__TE_______EE____AA_A_____E___A____T__TT_EE__A_T_
__E__E___E_T____TTA_E___ETA___ET_E_A__E__A_____E_E_E_T
TAE___A__________E_TA____T_EE_E_E_T_A_T_EA__________E_
_A____T___E_____ATAT_E___TEE_T__AA_____AA__TT_ET_____T
E_T_E___E__TA___TA_A______E_________E_T__TA_ETT_E____E
_A_T_E_AA_A_______T_E_E_____E______ET_E____E_A_T_E_TE_
__T__T_AA_

Additionally we can do this with two letter blocks and three letter blocks. That needs a little bit of time of course but it is not too hard and it gets easier when you have more text as the frequency test becomes more accurate.

I encourage you to try it out for a little bit to crack the code at this point. If you get stuck at some point you can of course first cheat by checking the version with spaces... but you can also at some point brute force it after you have removed enough uncertainty. If you know 16 chars for sure you just need about 4 million brute force steps to check the rest and of course at some point you'll be just able to read it even if some chars are still unclear.

The next method is called the Vigenère cipher which is build on top of the Caesar method but is aware of the frequency trick. It uses a keyword like "OPENSOURCES" and then shifts the first letter by 14 spots (O is the fivetenth letter in the alphabet) then shifts the second letter by 15 spots (P is the sixteens one) and so on. After the keyword is done it will we used again.

In action:

KEY:    OPENSOURCESOPENSOURCESO
Plain:  MYSECRETMESSAGEANDYOURS
Cipher: ANWRUFYKOIKGPKRSBXPQYJG

This is of course better because the same letter like the four S in our text are encrypted to four different letters WIKG. It is also very simple to use and decryption is just shifting backwards.

In this short plain text and relatively long keyword it is a good method but for longer texts there are some problems:

Do I use keywords from a dictionary?
- Then with a computer you just need to test them all :D
How long or short is the keyword?

Well I should mention that the method is from the 16th century so they probably didn't think much about computers at that time.

Nevertheless after 300 years it got cracked. The keyword repeats so by luck there are cases that the same word gets encrypted at the same position relative to the keyword and you can work with frequency analysis again.

I think that should be enough history for now.

How does the Enigma work?

First of all it is a machine so we don't have to do the operations by hand anymore. For the Vigenère cipher it was important that it is not too hard to encrypt and decrypt the messages if you know the key. With the Enigma it would bit harder to do it by hand but with a machine nobody has to think about that anymore.

Let's have a look at a visualization of an encryption step while explaining it.

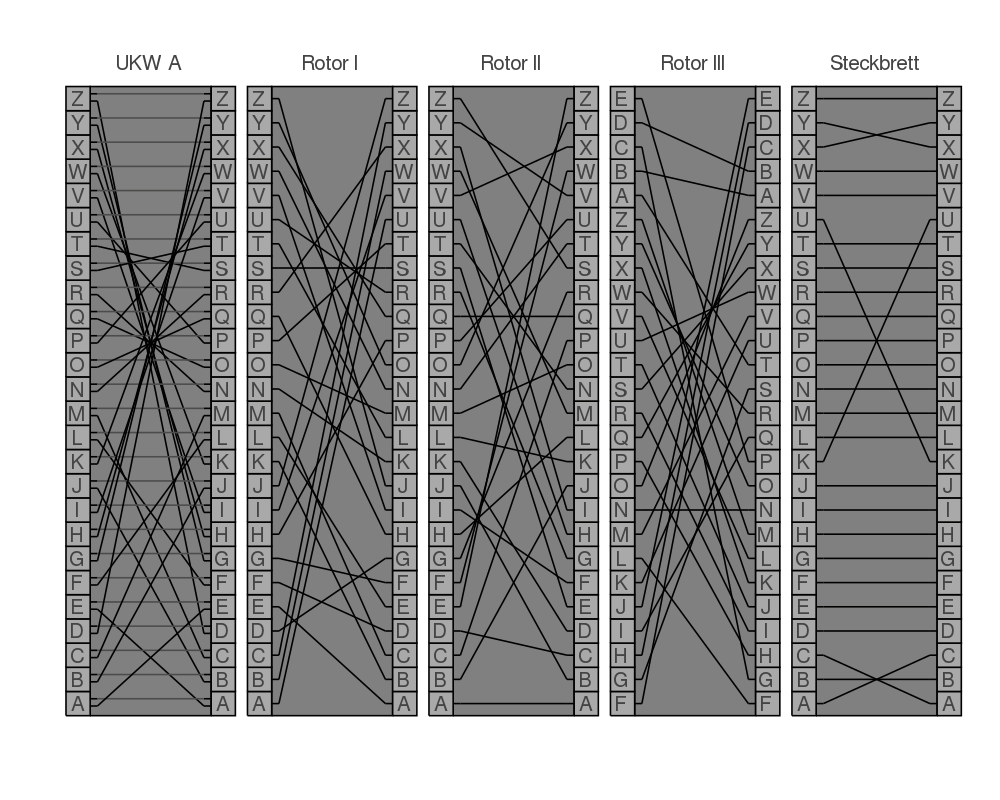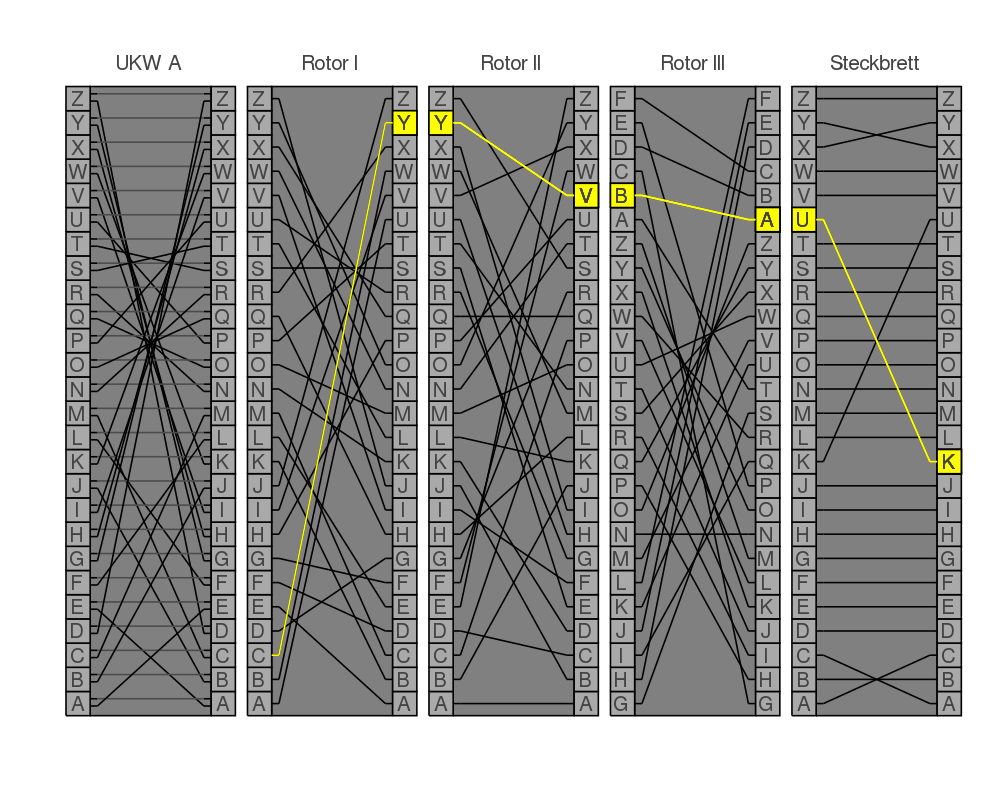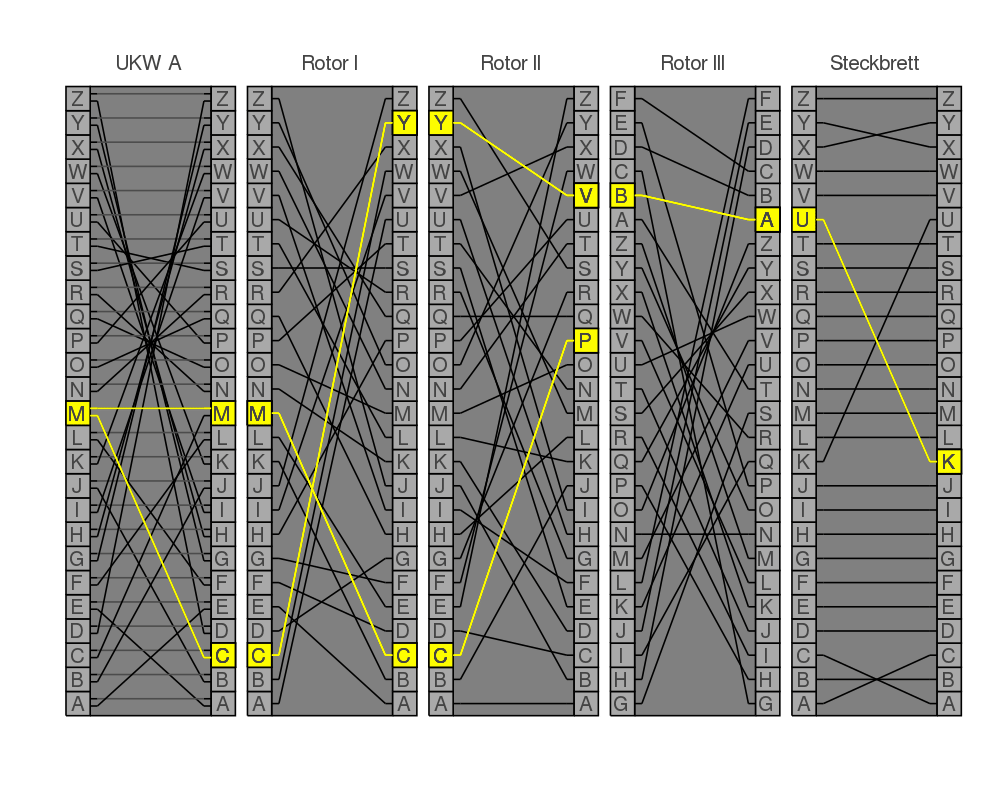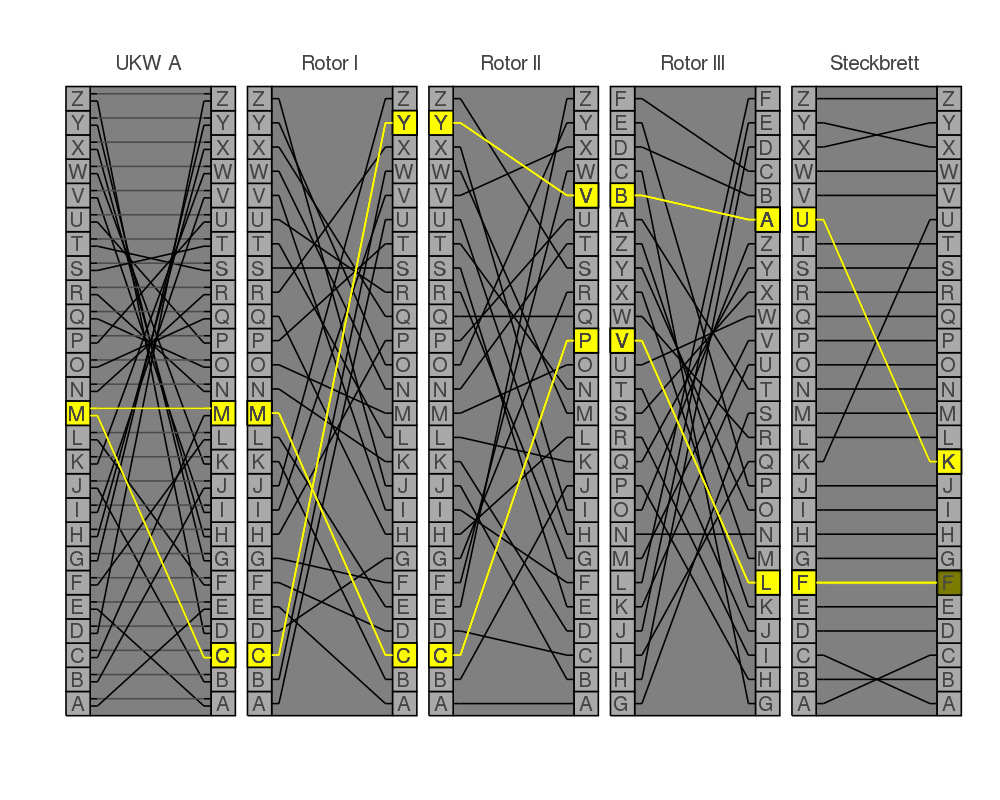
First of all we have 5 encryption steps: UKW (Umkehrwalze = reflector), 3 rotors and the plugboard (Steckbrett in German).

We move from right to left and then back. Entering K into something like a typewritter triggers the right most rotor to move one step. Then the letter K goes a swapping board which swaps some letters with other and is symmetric here. In the gif we only have three of those swaps. Then the signal goes into the first rotor (from the right) and enters at position A because of the rotation step and gets out at B because the rotor is just mapping each letter to a different one. Then it goes through the second and third rotor. A C enters the reflector which is basically also just a mapping and then goes back through all three rotors and the plugboard and then a lightbulb lights up and shows us the letter F.

If we only had those steps without rotor rotation it would be just a simple mapping like the one you will crack the next days. ;) Because we have the rotating rotors the mapping changes every time a bit similar to the Vigenère cipher. After the right most rotor did some steps the middle rotor rotates one position and then after some more strokes the left most rotor steps one step forward. Similar to a second, minute and hour hands on a clock.

The settings

We should talk a bit about all the things the Germans could change so the settings of the machine. First of all the plugboard (Steckbrett). They would normally set 10 (or somewhere I saw 6) plugs which means that swap two letters. For the calculation I'll use 10 and for coding I don't care about how many are used at the moment. Then they had some rotors that they could slide into the position. For different purposes and different times that number ranged from 5 to about 8. I used the somewhat standard 5. Then there are three possible reflectors to choose from (in my version at least :D).

This reduces the number of general possibilties of course but it needed to be practiable for the Germans.

That means we have \(3 \cdot 5 \cdot 4 \cdot 3 = 180\) possibilities for which rotors we use and at which position and three for the reflectors. Then we give the rotors a starting positon from which they start to rotate which are \(26\) for each of them.

\[ 3 \cdot (5 \cdot 26) \cdot (4 \cdot 26) \cdot (3 \cdot 26) = 3163680 \]

That is still a relatively small number and then the plugboard hits us.

We have 26 letters which we can arrange in \(26!\) positions. Then we have 6 letters which are not connected. This gives us \(\frac{26!}{6!}\) combinations. Second thing is that we don't care about the order of the swaps which are \(10!\) ways. Additionally we have a symmetric swap so "A" <-> "B" is the same as "B" <-> "A" (2 arrangements for each plug). Because we have 10 of those pairs we have \(2^{10}\) possibilities that we don't care about.

In total that gives us:

\[ \frac{26!}{6!\cdot 10! \cdot 2^{10}} = 150,738,274,937,250 \]

Combined with our small millions from the beginning we get.

\[ 3 \cdot (5 \cdot 26) \cdot (4 \cdot 26) \cdot (3 \cdot 26) \cdot \frac{26!}{6!\cdot 10! \cdot 2^{10}} = 158,962,555,217,826,360,000 \]

Well in comparison to our \(26!\) at the beginning it is not that big but it doesn't have the frequency flaw.

PLAIN:  OLEKR OLEKR OLEKR OLEKR OLEKR OLEKR OLEKR
SECRET: ZRINE YRMQB MGTDW AEBMM KCCXU WXCNV ZAUJO

It doesn't repeat itself and well the Germans thought it is the best cipher ever.

Coding the Enigma Machine

Before we start to think about flaws and how to crack the machine we should first make a replica. As we are living in the computer era we don't actually have to build one of those machines we just have to code it.

I've created a Julia package for it but don't want to discuss that here again as I did it in the first part of the constraint solver series.

We have a src/Enigma.jl and I've created three structs:

mutable struct Rotor
    name            :: String
    order           :: Int # indicates whether it's the 1st, 2nd, 3rd rotor
    mapping         :: Vector{Int}
    mapping_bw      :: Vector{Int}
    position        :: Int
    rotation_point  :: Int
end

mutable struct UKW
    name            :: String
    mapping         :: Vector{Int}
end

mutable struct EnigmaMachine
    plugboard       :: Vector{Int}
    rotors          :: Tuple{Rotor,Rotor,Rotor}
    ukw             :: UKW
end

which define the Enigma machine. The rotors have a mapping in the forward direction and for the way after the ukw (reflector) they run in the backward directon. For the UKW we have a struct as well, as it gets a name and for the Plugboard we simply store the mapping instead of all the plugs.

One thing I didn't talk about before is that the rotors don't make a full rotation every time and then the next rotor rotates by one step but instead each rotor has a rotation point where the next rotor in line is triggered.

Edit: 12.02.2020 Updated the structure of the const. See PR #11

const possible_ukw = [
    Dict(:name => "A", :mapping => [05, 10, 13, 26, 01, 12, 25, 24, 22, 02, 23, 06, 03, 18, 17, 21, 15, 14, 20, 19, 16, 09, 11, 08, 07, 04]),
    Dict(:name => "B", :mapping => [25, 18, 21, 08, 17, 19, 12, 04, 16, 24, 14, 07, 15, 11, 13, 09, 05, 02, 06, 26, 03, 23, 22, 10, 01, 20]),
    Dict(:name => "C", :mapping => [06, 22, 16, 10, 09, 01, 15, 25, 05, 04, 18, 26, 24, 23, 07, 03, 20, 11, 21, 17, 19, 02, 14, 13, 08, 12])
]

const possible_rotors = [
    Dict(:name => "I", 
         :mapping => [05, 11, 13, 06, 12, 07, 04, 17, 22, 26, 14, 20, 15, 23, 25, 08, 24, 21, 19, 16, 01, 09, 02, 18, 03, 10],
         :rotation_point => 18),
    Dict(:name => "II",
         :mapping => [01, 10, 04, 11, 19, 09, 18, 21, 24, 02, 12, 08, 23, 20, 13, 03, 17, 07, 26, 14, 16, 25, 06, 22, 15, 05],
         :rotation_point => 6),
    Dict(:name => "III",
         :mapping => [02, 04, 06, 08, 10, 12, 03, 16, 18, 20, 24, 22, 26, 14, 25, 05, 09, 23, 07, 01, 11, 13, 21, 19, 17, 15],
         :rotation_point => 23),
    Dict(:name => "IV",
         :mapping => [05, 19, 15, 22, 16, 26, 10, 01, 25, 17, 21, 09, 18, 08, 24, 12, 14, 06, 20, 07, 11, 04, 03, 13, 23, 02],
         :rotation_point => 11),
    Dict(:name => "V",
         :mapping => [22, 26, 02, 18, 07, 09, 20, 25, 21, 16, 19, 04, 14, 08, 12, 24, 01, 23, 13, 10, 17, 15, 06, 05, 03, 11],
         :rotation_point => 1)
]

This defines the mappings of the rotors and the reflectors and the rotation points. ~~I should probably move the rotation points into the possible_rotors const but well as always this just a snapshot of the project ;)~~

Oh and I moved from "ABC" to "01 02 03" of course.

We want to define the EnigmaMachine by the rotors used (from left to right) the reflector as well as the rotor positions.

function EnigmaMachine(r1::Int, r2::Int, r3::Int, ukw::Int; p1=1, p2=1, p3=1)
    rotor_1 = Rotor(possible_rotors[r1][:name], 1, possible_rotors[r1][:mapping], p1, possible_rotors[r1][:rotation_point])
    rotor_2 = Rotor(possible_rotors[r2][:name], 2, possible_rotors[r2][:mapping], p2, possible_rotors[r2][:rotation_point])
    rotor_3 = Rotor(possible_rotors[r3][:name], 3, possible_rotors[r3][:mapping], p3, possible_rotors[r3][:rotation_point])

    return EnigmaMachine(collect(1:26), (rotor_1,rotor_2,rotor_3), UKW(possible_ukw[ukw][:name], possible_ukw[ukw][:mapping]))
end

Then we have some functions like EnigmaMachine() for a default machine, set_rotors! to change the rotors used and so on. I'll make a documentation availbable soon :)

Oh yeah the whole project is of course open source as this is the opensourc.es blog! => Enigma.jl

Let's start with encrypting a letter. Then we just have to apply that for a text and for decrypting we can call the same method as it is symmetric.

function encode_single_idx_to_idx(enigma::EnigmaMachine, number::Int)
    number = enigma.plugboard[number]
    step_rotors!(enigma)
    for i=3:-1:1
        r = enigma.rotors[i]
        number = index_connected_to(r, number)
    end
    number = enigma.ukw.mapping[number]
    for r in enigma.rotors
        number = index_connected_to(r, number; backward=true)
    end
    number = enigma.plugboard[number]
    return number
end

This takes a number from 1-26 now and outputs a number in the same range. The first and last step in the function are simple. We go into the plugboard and out. The second step is to step the rotors. There we need to handle that the next rotor is moved when we reach the rotation point. Then we move from right to left through the rotors have the simple reflector step and move back.

The a bit more complicated function is index_connected_to. There I used the method seen in the gif.

that we don't care about the current letter but instead work with the position we get in and get out. So in the gif we enter at index 21 (counting from bottom to top) which is the A and get out at position here B.

We have one way for forward and backward which only changes whether we use .mapping or .mapping_bw of the rotor.

function index_connected_to(rotor, index; backward=false)
    index = (index+25+rotor.position-1) % 26+1
    if !backward
        through_rotor = rotor.mapping[index]
    else
        through_rotor = rotor.mapping_bw[index]
    end
    result = through_rotor-rotor.position+1
    result = (result-1 + 26) % 26 + 1
    return result
end

First we shift the index according to the rotor position and we want to get a number between 1-26 again because Julia is one index based. Therefore we need the % 26 + 1 in the end. I also found that in Julia as well as in all other languages I've checked -5 % 26 = -5 but in Python it is 21 which would be handy here but somehow I expected it to be -5. It was just a moment where I though: Yeah Python is convenient. Well Here I just add 25 to the equation to never be negative. You might think well the index is always at least 1 and the rotor position too? Well I used that the rotor position can be 0 which reprents 26 as there I used % 26 :D Yeah that maybe was a stupid way to switch from 1 based indexing to 0 based but: "DEAL WITH IT!" or make a PR ;) (Done PR #11)

Edit 12.02.2020 Now it looks like this (after setting the rotation points to be 1-26)

function index_connected_to(rotor, index; backward=false)
    # index and rotor position are 1 index based
    # turning the rotor back to get the actual index
    index = (index-1+rotor.position-1) % 26+1
    if !backward
        through_rotor = rotor.mapping[index]
    else
        through_rotor = rotor.mapping_bw[index]
    end
    # turning the rotor again to translate the index into the next rotor
    result = through_rotor-rotor.position+1
    result = (result-1 + 26) % 26 + 1
    return result
end

The first line there changes everything to a form where the rotor would never rotate and starts at A then we can move through the rotor and in the end we have to shift again because the rotate well rotated.

The last step is simple but for me a bit confusing: Stepping the rotors.

Edit 12.02.2020 Changed such that the rotation point is from 1-26 now.

function step_rotors!(enigma::EnigmaMachine)
    # right most rotor
    enigma.rotors[3].position += 1
    enigma.rotors[3].position == 27 && (enigma.rotors[3].position = 1)
    if enigma.rotors[3].position == enigma.rotors[3].rotation_point
        enigma.rotors[2].position += 1
        enigma.rotors[2].position == 27 && (enigma.rotors[2].position = 1)
        if enigma.rotors[2].position == enigma.rotors[2].rotation_point
            enigma.rotors[1].position += 1
            enigma.rotors[1].position == 27 && (enigma.rotors[1].position = 1)
        end
    elseif enigma.rotors[2].position+1 == enigma.rotors[2].rotation_point
        enigma.rotors[2].position += 1
        enigma.rotors[2].position == 27 && (enigma.rotors[2].position = 1)
        enigma.rotors[1].position += 1
        enigma.rotors[1].position == 27 && (enigma.rotors[1].position = 1)
    end
end

Everything is simple until the elseif. ~~We just move forward get a number between 0-25 this time and when we are at the rotation point we move the next rotor. Yeah I realize it was stupid to start at 0 because if the rotation point is 'Z' we would need to write a 0. Okay I'll fix that one day :D~~ Fixed!

The elseif statement is there for the so called double stepping which means that the middle rotor makes onee normal step when it gets triggered by the right most rotor but in the next move it steps again and then waits for another 24 steps waiting to get triggered again. I didn't know about it and tried to verify that my implementation is correct by checking it against other simulators on the internet and finally I found that this thing exists.

Alright we can decode single letters or well numbers. For letters we need:

function encode_single(enigma::EnigmaMachine, c::Char)
    number = Int(c)-64
    number = encode_single_idx_to_idx(enigma, number)
    return Char(number+64)
end

and just call it several times for a string. Done!

Additionally we output it as blocks of 5 uppercase letters as this was done during the war.

function enigma_styled_text(text::String)
    return string(strip(replace(uppercase(replace(text, r"[^a-zA-Z]"=>"")), r"(.{5})" => s"\1 ")))
end

The Bombe

After about 20 minutes we are finally at the actual goal of this post. After seeing the Code Bullet video where he said that he tries to crack it but actually until now never did a video about it I thought: Well coding up the machine wasn't that hard in retrospect. (But I had a lot of bugs like the double stepping one.) I wanted to be able to decipher enigma text as I somewhat understood the methods for Caesar and for the Vigenère cipher and how to at least theoretically crack them. A couple of years ago I also coded something for the Vigenère cipher if I remember correctly... Well for Enigma I heard some theories about how it was cracked but I never fully got it.

For me the best way to understand it is to code it so here we are. Before we code things up we should get the flaws and how to use them. (Yes I should have done that better myself. I of course got so into it and just coded up some stuff which was slow but somewhat worked...)

A main flaw was that a letter got never encrypted by itself. This means that if we get:

SECRET: DXPON HBODJ UUXHI IXZED UHTGF NHLNP IAX

and know that the word: Wetterbericht (German for weather report) is part of that text we can slide it over the text.

SECRET: DXPONHBODJUUXHIIXZEDUHTGFNHLNPIAX
GUESSS: WETTERBERICHT

this for example does not work because the B would be encrypted as a B. That means the word can't be at that position.

Maybe I should mention that my machine Bombe (name from the original machine Alan Turing constructed Bombe Wikipedia) can only crack the code if we have a hint like Wetterbericht.

Let's assume that Wetterbericht is at the fourth position for now. As there are no single letter words in German and the thrid position doesn't work because of the H.

SECRET: DXPONHBODJUUXHIIXZEDUHTGFNHLNPIAX
GUESSS:    WETTERBERICHT

The next thing is that we check which letter is used most often in that range which should be the Ts of Wetterbericht.

They got encrypted to H, B and I. (By got encrypted I mean if we know that Wetterbericht is at that position.)

Now we make some more guesses. We assume that a plug on the plugboard connects T with A and we know that the rotors used are 1,2,3 at position 1,1,1 and reflector A.

Haha really? We basically assume we know everything? Actually yes. Later we try all the 3 million possibilities and only care about the plugboard here.

In the package that would be

enigma = EnigmaMachine();
set_rotors!(enigma, 1,2,3);
set_rotor_positions!(enigma, 1,1,1);
set_ukw!(enigma, 1);
set_plugboard!(enigma, "AT");

Then we move the rotors by 5 steps to get to the first T.

for i=1:5
    Enigma.step_rotors!(enigma)
end

Next we type T and get R as a result.

println(encode!(enigma, "T"))

Remember that we assume that we know everything but the plugboard. Now we've got a "J" but in the secret message there is an "H" at that positon. Therefore we can deduce that on the plugboard "J" must be connected to "H".

List of deductions if T <-> A

J <-> H

Have a look at our secret again:

SECRET: DXPONHBODJUUXHIIXZEDUHTGFNHLNPIAX
GUESSS:    WETTERBERICHT

Okay let's do the same for our next T after setting the plugboard:

set_plugboard!(enigma, "AT RH");
encode!(enigma, "T")

Result: N but should be B =>

List of deductions if T <-> A

J <-> H
N <-> B

Know we know that N <-> B therefore we can also check the E in front of the TT sequence of Wetterbericht as we know that that E should be connected to N which means if we type in N it should result in E.

We have to set our rotor positions accordingly:

set_plugboard!(enigma, "AT JH NB");
set_rotor_positions!(enigma, 1,1,1);
for i=1:4
    Enigma.step_rotors!(enigma)
end
encode!(enigma, "N") # => P but should be E

List of deductions if T <-> A

J <-> H
N <-> B
E <-> P

The E itself gives us even more to check as there are another two "E" in Wetterbericht.

Have a look at our secret again:

SECRET: DXPONHBODJUUXHIIXZEDUHTGFNHLNPIAX
GUESSS:    WETTERBERICHT

We can check the E after TT.

set_plugboard!(enigma, "AT JH NB EP");
set_rotor_positions!(enigma, 1,1,1);
for i=1:7
    Enigma.step_rotors!(enigma)
end
encode!(enigma, "E") # => B but should be O

List of deductions if T <-> A

J <-> H
N <-> B
E <-> P
B <-> O

Finally we can deduce that T is not connected to A or that our rotor settings are wrong (which we don't believe for now). The reason we can deduce that is that 2. and 4. are contradictorily because B can be only connected to one of N and O.

Therefore we can set the plug to T <-> B and try again and maybe all up to T <-> Z fail. Then we can use the next rotor setting and try again.

If that all fails we move to the next position. How long does it take to crack it?

I'm currently letting it run and it runs for about 25 Minutes now but we can make an estimate while it runs for a bit longer.

During the implementation I estimated that it will take half a day with my worse method to check for a single position so if we know "Wetterbericht" is the start of the message. Therefore I implemented that the user can specify some known setting such that I can play a little bit in a matter of seconds or some minutes.

Let's create a new secret for this one with the following settings:

enigma = EnigmaMachine();
set_plugboard!(enigma, "AT RH MV QZ LP");
set_rotors!(enigma, 1, 3, 4)
set_ukw!(enigma, 2)
encode!(enigma, "This is the weatherreport for today. It will rain")

Secret:

OPKFF VNRUM DHGGU JVZRP JXPDS HVYYZ HUXLS CQULM

If we know the setting we can configure our Bombe accordingly:

bombe = BombeMachine("OPKFF VNRUM DHGGU JVZRP JXPDS HVYYZ HUXLS CQULM", "Weatherreport");
set_possible_rotors!(bombe, 1, 3, 4);
set_possible_ukws!(bombe, 2);
@time enigmas = run_cracking(bombe; log=false);

This takes about 20 seconds. Now we have 60 possible rotor combinations and 3 for the reflector so can multiply that by 180 and get 3600 seconds so an hour.

BTW my run just finished in 30 minutes. It of course always depends on how many possible positions for the word exist which depend on the length of the secret and on the settings as well. The run returned 603 enigma machines.

One catch at the end that I should mention: Sometimes we don't get the complete setting of the plugboard as we can only deduce some of the settings. This means that if the actual setting of the plugboard is "AT BQ MV OS" and for the hint we only use "AT BQ MV" the method just returns that and you might need to try the rest yourself or you can enable a setting in my code with:

enable_ambiguous!(bombe)

to run all those settings and add it to the list of returned enigma machines. This often takes much longer so I disabled it by default and often you can read the text even without that because only a few letters are swapped by that.

I think the running time is okayish. There are some more things I have in mind to reduce the time but I'm already quite happy with the result.

It's already a long post so I'll implement that we have rotor positions from 1-26 instead of a weird 0 for 'Z' and implement the speedup I have in mind and maybe go through the code of the Bombe next time. I also want to make a small video with explanations and visualizations for it but wanted to finish this blog post first.

If you have further suggestions please let me know via E-Mail o.kroeger@opensourc.es or Twitter @opensourcesblog or open an issue at the repo.

Hope you enjoyed this post and if you come here often please consider supporting me via Patreon or GitHub sponsors that would mean a lot to me.

You'll get posts earlier and sometimes there are specials like giving you a sight of the new blog structure I'm planning.

OpenSourc.ES

Building an Enigma emulator and a Bombe

A bit of a story

How does the Enigma work?

The settings

Coding the Enigma Machine

The Bombe

Further reading/watching