Speeding up my julia code for the hungarian method
Creation date: 2019-04-03
A few days ago I had a look at my hungarian method project again. You can find the blog post here. After writing that blog post the owner of the julia library for that algorithm commented on my post and made a huge performance improvement to his library to be much faster than my code where my goal of actually implementing it was to be faster to compete in this kaggle challenge. He also gave me some performance tips which I wanted to test.
You can of course just read this article for the performance improvements but if you want to know more about the hungarian method please read my previous post about it. Okay... a short version: The hungarian method is an algorithm which finds the minimal sum in a square matrix given the constraint that each row and each column has exactly one chosen value. In my example I had 5 kids and 5 gifts and each kid and each gift has a ranking for the gifts and kids respectively. I want to get the best kid <-> gift combination to make the kids, gifts as happy as possible. Yes it's a bit weird but quite funny ;)
Before I start I have to actually change some code of the hungarian method to be compatible with Julia v1.0 and not Julia v0.6 which I used back then.
Changes:
seed = srand(...)tousing Randomand thenseed = Random.seed!(...)gc()toBase.GC.gc()A[A .> 50000] = 50000toA[A .> 50000] .= 50000in general in quite some places changes
-to.-or+to.+etc whenever the right hand side must be broadcasted.
findtofindallhere for 2D arrays you get
CartesianIndexwith(y,x)instead of a single coordinate.
so this:
function get_matching(mat)
# create bipartite matching graph
zero_vals = find(x->x==0,mat)
ei = Vector{Int64}()
ej = Vector{Int64}()
for i in zero_vals
# zero based
zi = i-1
zr = zi % size(mat)[1]
push!(ej,zr+1) # row
push!(ei,div((zi-zr),size(mat)[1])+1) # col
end
matching = bipartite_matching(ones(Int64,length(ei)), ei, ej)
return matching
endwill be:
function get_matching(mat)
# create bipartite matching graph
zero_vals = findall(x->x==0,mat)
ei = Vector{Int64}()
ej = Vector{Int64}()
for yx in zero_vals
push!(ej,yx[1]) # row
push!(ei,yx[2]) # col
end
matching = bipartite_matching(ones(Int64,length(ei)), ei, ej)
return matching
endwhich is actually much easier to read.
Now the current benchmark with the new version of the Hungarian Method library:
| Matrix size | Lib seconds | Lib memory | Own seconds | Own memory |
|---|---|---|---|---|
| 800 | 0.15 | 1.4MiB | 2.78 | 1.7GiB |
| 1000 | 0.2 | 2.1MiB | 4.57 | 2.1GiB |
| 2000 | 0.51 | 7.9MiB | 12.5 | 4.9GiB |
| 4000 | 1.22 | 31.2MiB | 29.4 | 10.6GiB |
| 8000 | 3.8 | 123.2MiB | 65.8 | 20.9GiB |
first of all the library is always faster and uses less memory and in both cases I mean much faster and way less memory. The library is about 20 times faster and uses \(\approx 170\) times less memory. By memory I always refer to memory allocation during the process. At no point of my algorithm is actually 20GiB used.
First I want to know why my code is using so much memory. You can do this by running julia by calling julia --track-allocation=user. You should then run a quite fast version of your algorithm as this takes quite some time. Therefore I only run it with n=800. Now running the library version takes about 6 seconds instead of 0.15... anyway waiting a while until mine finishes.
If you close your julia command line you see that a file for each julia file is created which shows you how much memory is used by each line in your program. Each line shows you the number of bytes allocated.
Okay now my run is done (115s). Let's have a look at the file.
At the beginning there is an obvious line:
1280080 mat = copy(mat_original)which are 1.28MB and we probably don't really need this if we are okay with the fact that our method changes the original input. Anyway the whole process for a 800x800 matrix uses over 1.5GiB which means this isn't that important.
- # subtract col minimum
0 for c=1:size(mat)[2]
2892800 mat[:,c] .-= minimum(mat[:,c])
- endOkay this seems to be a bit strange to me as I didn't expect that uses actually memory. Then we have
10992875 sorted_matching = sort(matching.match)[1:matching.cardinality]which is also more then expected. Here I can see that the array is sorted completely and then we take the first elements which seems a bit wasteful so we might wanna have a look into it later.
Now something really interesting:
144597824 idx_not_marked_cols = findall(x->!x,cols_marked)This gets called often and uses about 150MB in total which is quite a bit. This should be fixed! We have the same for rows_marked later on again and then this is super wasteful and I didn't expect this:
136398720 min_val = minimum(mat[mask])
577316080 mat .-= min_val*maskso probably we shouldn't use this type of mask and we have it again here:
577316080 mat .+= min_val*maskIn general it might be reasonable to use @views when actually a view of a matrix can be used and not copying it like here:
- # subtract col minimum
0 for c=1:size(mat)[2]
115200 @views mat[:,c] .-= minimum(mat[:,c])
- endThat are quite easy fixes. Additionally for the sorting I use sorted_matching = partialsort(matching.match, 1:matching.cardinality) which only partially sorts the array.
But now to the more interesting stuff with the mask. Let's have a deeper look into it to actually see what we want to do again:
mask[:,:] = true
mask[:,marked_col_ind] = false
row_mask[:] = true
row_mask[marked_row_ind] = false
mask[row_mask,:] = false
min_val = minimum(mat[mask])
mat .-= min_val*mask
mask[:,:] = true
mask[marked_row_ind,:] = false
col_unmask[:] = true
col_unmask[marked_col_ind] = false
mask[:,col_unmask] = false
mat .+= min_val*maskWe have a mask which we use to mark all fields which we want to use for getting the minimum and the subtract or add them to some rows and columns.
First I want to create a representation of marked columns/rows and unmarked columns/rows basically just a list of indices for each and a different representation when building where I set a row to marked or not so a boolean array. Then I can later iterate over all unmarked columns and then marked rows to get the minimum value instead of doing this mask thing as the mask uses a lot of memory and is slowing things down as the mask is not "random" but actually very well structured. I mentioned in my previous post that I want to use a mask as I thought loops are slow but actually they aren't :D (at least in julia).
First I declare these arrays:
ind_marked_rows = zeros(Int64, nrows)
ind_unmarked_rows = zeros(Int64, nrows)
ind_marked_cols = zeros(Int64, ncols)
ind_unmarked_cols = zeros(Int64, ncols)and then fill them:
ind_marked_rows_end = 0
ind_unmarked_rows_end = 0
for r=1:nrows
if rows_marked[r]
ind_marked_rows_end += 1
ind_marked_rows[ind_marked_rows_end] = r
else
ind_unmarked_rows_end += 1
ind_unmarked_rows[ind_unmarked_rows_end] = r
end
end
ind_marked_cols_end = 0
ind_unmarked_cols_end = 0
for c=1:ncols
if cols_marked[c]
ind_marked_cols_end += 1
ind_marked_cols[ind_marked_cols_end] = c
else
ind_unmarked_cols_end += 1
ind_unmarked_cols[ind_unmarked_cols_end] = c
end
endwhich basically uses the idea that I want to have a fixed sized length of arrays to not create a vector each time but of course sometimes 10 rows are marked and 5 are unmarked (for a 15x15 matrix) and sometimes it's 7 and 8 respectively or something like that. Therefore I fill the array each time from the beginning and just have an index variable for up to which index this array is actually correct and the rest should be ignored. Then I create views of those arrays which only show the relevant indices:
@views ind_marked_rows_sub = ind_marked_rows[1:ind_marked_rows_end]
@views ind_unmarked_rows_sub = ind_unmarked_rows[1:ind_unmarked_rows_end]
@views ind_marked_cols_sub = ind_marked_cols[1:ind_marked_cols_end]
@views ind_unmarked_cols_sub = ind_unmarked_cols[1:ind_unmarked_cols_end]Then I use this code to actually determine the minimum and subtract and add the minimum to part of the arrays.
start_timer = time()
#minimum where !cols_marked but rows_marked
@inbounds @views min_val = minimum(mat[ind_marked_rows_sub,ind_unmarked_cols_sub])
find_min_total_time += time()-start_timer
start_timer = time()
# subtract minimum from this mask
@inbounds for c in ind_unmarked_cols_sub
for r in ind_marked_rows_sub
mat[r,c] -= min_val
end
end
sub_min_total_time += time()-start_timer
start_timer = time()
# add minimum where !rows_marked but cols_marked
@inbounds @views mat[ind_unmarked_rows_sub,ind_marked_cols_sub] .+= min_val
add_min_total_time += time()-start_timeralso measuring some extra timings.
Creating a new benchmark table...
| Matrix size | Lib seconds | Lib memory | Own seconds | Own memory |
|---|---|---|---|---|
| 800 | 0.15 | 1.4MiB | 1.14 | 426MiB |
| 1000 | 0.2 | 2.1MiB | 1.85 | 588MiB |
| 2000 | 0.51 | 7.9MiB | 4.7 | 668Mib |
| 4000 | 1.22 | 31.2MiB | 14 | 1.146GiB |
| 8000 | 3.8 | 123.2MiB | 28.6 | 1.78GiB |
That is definitely quite an improvement. It is more than twice as fast and uses less than half of the memory. Nevertheless nobody should use it as it is still way slower than the library. Shell I leave it like that?
Of course not. Let's have a look at our extra timings. This is for 8000x8000 matrix:
Own:
Total inner while time: 13.692403078079224
Total create_ind_vect_total_time: 0.0055692195892333984
Total find_min_total_time: 2.1337521076202393
Total sub_min_total_time: 1.0597960948944092
Total add_min_total_time: 1.2120177745819092
c_outer_while: 74
c_inner_while: 4781
28.614113 seconds (247.27 k allocations: 1.775 GiB, 0.80% gc time)This shows that we use about half of the time in the inner while loop then about 1/6 of the whole time in finding the minimum and subtracting/adding it. Where do we actually spend the other third?
We actually need about 8s in this line zero_vals = findall(x->x==0,mat) which is part of get_matching which we call 74 times. Don't remember anymore how much memory it actually used but we know that the other findall calls used quite a bit. Let's have a look at the inner loop first as it uses the most time:
changed = true
while changed
c_inner_while += 1
changed = false
new_marked_col_ind = Vector{Int64}()
# mark cols
in_start = time()
idx_not_marked_cols = findall(x->!x,cols_marked)
@inbounds for c in idx_not_marked_cols
@inbounds for r in new_marked_row_ind
@inbounds if mat[r,c] == 0
cols_marked[c] = true
push!(marked_col_ind,c)
push!(new_marked_col_ind,c)
break
end
end
end
new_marked_row_ind = Vector{Int64}()
idx_not_marked_rows = findall(x->!x,rows_marked)
# mark new rows
@inbounds for r in idx_not_marked_rows
@inbounds for c in new_marked_col_ind
@inbounds if matching.match[c] == r
rows_marked[r] = true
push!(marked_row_ind,r)
push!(new_marked_row_ind,r)
changed = true
break
end
end
end
endFirst of all we don't need marked_row_ind and marked_col_ind anymore as we created something similar with our _sub arrays explained above. This doesn't give any speed up gain but is simply not necessary. Here:
@inbounds for c in idx_not_marked_cols
@inbounds for r in new_marked_row_ind
@inbounds if mat[r,c] == 0
cols_marked[c] = true
push!(marked_col_ind,c)
push!(new_marked_col_ind,c)
break
end
end
endwe can see that we also are interested in the 0s of mat same as before. We can compute the zeros once in the outer while loop and the use it for matching and for this inner while loop:
# mark cols
@inbounds for rc in matzeros
@inbounds if !cols_marked[rc[2]]
@inbounds if new_marked_row_ind[rc[1]]
cols_marked[rc[2]] = true
new_marked_col_ind[rc[2]] = true
end
end
endthis does the same as before if we crate the matzeros array and convert new_marked_col_ind into a boolean array. The complete while loop looks like this then:
while changed
c_inner_while += 1
changed = false
# mark cols
@inbounds for rc in matzeros
@inbounds if !cols_marked[rc[2]]
@inbounds if new_marked_row_ind[rc[1]]
cols_marked[rc[2]] = true
new_marked_col_ind[rc[2]] = true
end
end
end
# mark new rows
@inbounds for c in 1:ncols
r = matching.match[c]
@inbounds if new_marked_col_ind[c] && !rows_marked[r]
rows_marked[r] = true
new_marked_row_ind[r] = true
changed = true
end
end
endLet's have a look at our 8000x8000 example again:
Time for setup: 1.245980978012085
Total inner while time: 0.27219057083129883
Total create_ind_vect_total_time: 0.003743886947631836
Total find_min_total_time: 1.7174184322357178
Total sub_min_total_time: 1.067976713180542
Total add_min_total_time: 1.1212151050567627
Total zero_vals_total_time: 9.0477774143219
c_outer_while: 74
c_inner_while: 4781
14.729773 seconds (38.82 k allocations: 814.169 MiB, 1.22% gc time)It is again about twice as fast and uses about half of the memory it used before and is still about 5 times slower than the library :D Anyway we got from half of the time for the inner loop to about nothing Total inner while time: 0.27219057083129883. The library takes less than 4 seconds in total. Therefore we definitely have to cut down the time for finding the zeros as that takes 9s.
Let's think about that again. We get some input from the user in the beginning which means that we have to do it at least once as I still think that we need the zeros... okay but later on we might be able to figure out where the zeros actually are. We actually only add the minimum value somewhere and subtract it at some other positions of the array. Which means that only at the positions where we subtract a value there can be a new zero.
At the beginning we will have:
matzeros = findall(iszero, mat)
nmatzeros = length(matzeros)
max_nmatzeros = nmatzerosWhich means we are finding all zeros and save it and also save how many zeros we found both as the maximum zeros ever found and as the current index of the end similar to the _sub arrays we had before.
so we weill use:
@views matzeros_sub = matzeros[1:nmatzeros]in the beginning of the outer while loop.
Okay where is it possible to have zeros in the array? We have marked rows, unmarked rows, marked cols and unmarked cols and then the minimum is found and subtracted where !cols_marked but rows_marked and added where !rows_marked but cols_marked so we have two more possibilities one where both marked and one both unmarked and in these two cases we only have to check where there was a 0 before basically the unchanged zeros.
start_timer = time()
nmatzeros = 0
for matzero in matzeros_sub
if (rows_marked[matzero[1]] && cols_marked[matzero[2]]) || (!rows_marked[matzero[1]] && !cols_marked[matzero[2]])
nmatzeros += 1
if nmatzeros > max_nmatzeros
max_nmatzeros += 1
push!(matzeros, matzero)
else
matzeros[nmatzeros] = matzero
end
end
end
matzeros_total_time += time()-start_timerand for the new zeros we have:
# subtract minimum from this mask
@inbounds for c in ind_unmarked_cols_sub
for r in ind_marked_rows_sub
mat[r,c] -= min_val
if mat[r,c] == 0
nmatzeros += 1
if nmatzeros > max_nmatzeros
max_nmatzeros += 1
push!(matzeros, CartesianIndex(r,c))
else
matzeros[nmatzeros] = CartesianIndex(r,c)
end
end
end
endIn both cases we always have to check whether there are more zeros than before and if that is the case we have to extend the array.
okay new full benchmark table:
| Matrix size | Lib seconds | Lib memory | Own seconds | Own memory |
|---|---|---|---|---|
| 800 | 0.15 | 1.4MiB | 0.5 | 113MiB |
| 1000 | 0.2 | 2.1MiB | 0.7 | 134MiB |
| 2000 | 0.51 | 7.9MiB | 1.3 | 171Mib |
| 4000 | 1.22 | 31.2MiB | 2.8 | 314MiB |
| 8000 | 3.8 | 123.2MiB | 6 | 778MiB |
Again two times faster and half the memory :D We are getting closer and closer. A more detailed look again:
Own:
Time for setup: 1.3364341259002686
Total inner while time: 0.31391358375549316
Total matzeros_total_time: 0.005685091018676758
Total create_ind_vect_total_time: 0.003530263900756836
Total find_min_total_time: 1.609025001525879
Total sub_min_total_time: 1.3520302772521973
Total add_min_total_time: 1.1240284442901611
c_outer_while: 74
c_inner_while: 4416
5.979697 seconds (37.60 k allocations: 778.117 MiB, 3.01% gc time)Now actually the setup takes quite an amount and again finding the minimum and adding/subtracting it. I somehow assumed that the number of zeros decreases but to be sure I plotted it:
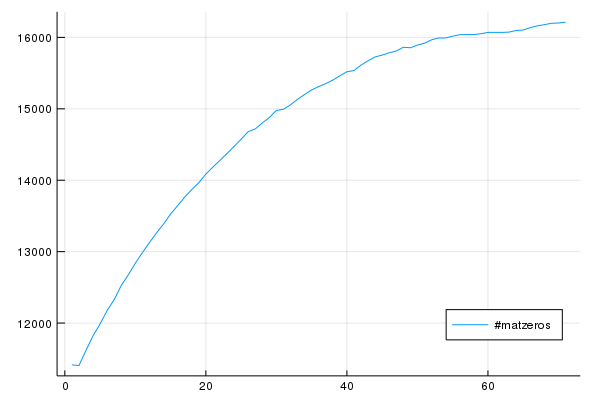
which shows me that I was totally wrong :D I should think about that again. So I could increase the array at the beginning to be twice as big but that is not faster as I think I have to fill it with something which takes time. I might think about that part again and maybe you can comment on this post if you have an idea or make a PR or open an issue ;)
Next part is to have a look at the setup time. Subtracting the col minimum and row minimum takes over 1.3s which seems quite a lot especially if you look at only the time for subtracting the column minimum which only takes 0.3s. I know that a matrix is stored column wise so this is a little bit expected.
I asked in the discourse forum and the best answer was to create this:
function subMins!(mat)
mcols = minimum(mat, dims=1)
for j = 1:size(mat,2), i = 1:size(mat,1)
mat[i,j] -= mcols[j]
end
mrows = minimum(mat, dims=2)
for j = 1:size(mat,2), i = 1:size(mat,1)
mat[i,j] -= mrows[i]
end
endnow for 8000x8000 it takes \(\approx 0.15s\) which is super nice and the memory allocation is much better as well from >700MiB to < 300MiB. As it now faster I want to test on bigger matrices as well so I introduce 16000x16000 and 20000x20000 and I removed the copying step in the beginning to indicate that I'm changing the input matrix I renamed the function to function run_hungarian!(mat) the ! indicates that the parameters might change.
| Matrix size | Lib seconds | Lib memory | Own seconds | Own memory |
|---|---|---|---|---|
| 800 | 0.15 | 1.4MiB | 0.5 | 107MiB |
| 1000 | 0.2 | 2.1MiB | 0.7 | 123MiB |
| 2000 | 0.51 | 7.9MiB | 1.3 | 132Mib |
| 4000 | 1.22 | 31.2MiB | 3 | 160MiB |
| 8000 | 3.8 | 123.2MiB | 5.7 | 228MiB |
| 16000 | 10.8 | 491.8MiB | 13.2 | 229MiB |
| 20000 | 17.8 | 777MiB | 18.05 | 223MiB |
I'm a bit confused why this takes longer for smaller matrices than before but anyway it's near the time of the library for bigger matrices and it uses less memory.
Let's have a look at the 20,000x20,000 matrix:
Own:
Time for setup: 1.0774140357971191
Total inner while time: 0.6575486660003662
Total matzeros_total_time: 0.008650541305541992
Total create_ind_vect_total_time: 0.004875898361206055
Total find_min_total_time: 5.690838813781738
Total sub_min_total_time: 4.94647216796875
Total add_min_total_time: 4.258580684661865
c_outer_while: 36
c_inner_while: 2743
18.052734 seconds (2.91 k allocations: 223.363 MiB, 1.66% gc time)Now I think finding the minimum takes too long as well as subtracting and adding it. :D Yes I'm jumping from one end to another but I hope you're still reading it ;)
We had:
#minimum where !cols_marked but rows_marked
@inbounds @views min_val = minimum(mat[ind_marked_rows_sub,ind_unmarked_cols_sub])and we can change it to:
#minimum where !cols_marked but rows_marked
@views mat_ind_unmarked_cols_sub = mat[:,ind_unmarked_cols_sub]
@views rmins = vec(minimum(mat_ind_unmarked_cols_sub[ind_marked_rows_sub,:], dims=2))
@views min_val = minimum(rmins)This gets a sub matrix by the columns which is fast and then minimizes over the marked rows and takes the minimum of that. In my test this reduces the time for finding the minimum from 5.7s to about 2.8.
I also replace:
@inbounds @views mat[ind_unmarked_rows_sub,ind_marked_cols_sub] .+= min_valby this and declare addition_vector = zeros(Int64, nrows) at the top.
addition_vector .= 0
addition_vector[ind_unmarked_rows_sub] .= min_val
@views mat_ind_marked_cols_sub = mat[:,ind_marked_cols_sub]
for col in eachcol(mat_ind_marked_cols_sub)
col .+= addition_vector
endwhich I think is sometimes slower and sometimes faster depending on how big ind_unmarked_rows_sub is but for this case it seems to be faster. Let's have a look at subtracting the minimum as well:
# subtract minimum from this mask
@inbounds for c in ind_unmarked_cols_sub
for r in ind_marked_rows_sub
mat[r,c] -= min_val
if mat[r,c] == 0
nmatzeros += 1
if nmatzeros > max_nmatzeros
max_nmatzeros += 1
push!(matzeros, CartesianIndex(r,c))
else
matzeros[nmatzeros] = CartesianIndex(r,c)
end
end
end
endthe problem here is that we not only subtract it but we also need to add the new zeros. I tried quite a bit with checking mat[r,c] == 0 only if the row has actually the correct minimum but it doesn't make anything faster.
Now the last thing I changed: We had this get_matching function:
function get_matching(matzeros_sub)
# create bipartite matching graph
ei = Vector{Int64}()
ej = Vector{Int64}()
for yx in matzeros_sub
push!(ej,yx[1]) # row
push!(ei,yx[2]) # col
end
matching = bipartite_matching(ones(Int64,length(ei)), ei, ej)
return matching
endthe problem here is that I push to a vector but I actually know how big the vector is. Therefore I use this now:
function get_matching(matzeros_sub)
# create bipartite matching graph
nmatzeros = length(matzeros_sub)
ei = zeros(Int64, nmatzeros)
ej = zeros(Int64, nmatzeros)
i = 1
for rc in matzeros_sub
ej[i] = rc[1] # row
ei[i] = rc[2] # col
i += 1
end
matching = bipartite_matching(ones(Int64,nmatzeros), ei, ej)
return matching
endLet's make a final benchmark table:
| Matrix size | Lib seconds | Lib memory | Own seconds | Own memory |
|---|---|---|---|---|
| 800 | 0.14 | 1.4MiB | 0.5 | 100MiB |
| 1000 | 0.19 | 2.1MiB | 0.55 | 117MiB |
| 2000 | 0.48 | 7.9MiB | 0.99 | 124Mib |
| 4000 | 1.14 | 31.2MiB | 2.09 | 153MiB |
| 8000 | 3.1 | 123.2MiB | 3.8 | 155MiB |
| 16000 | 10.1 | 491.8MiB | 8.6 | 197MiB |
| 20000 | 14.2 | 777MiB | 11.6 | 191MiB |
You might saw that the library is sometimes faster or slower than in previous runs as well this is due to some normal fluctuation as my computer is sometimes doing something else as well like playing music :/
Edit 04.04.2019 Gnimuc the owner of Hungarian.jl pointed out that I'm using the Hungarian.munkres function which makes a copy of the input instead of calling Hungarian.munkres! which works as run_hungarian!. Additionally I will use a different machine for running the benchmark which has more memory to try even bigger matrices. It is quite some pain to change all the tables which I had so far for this... So I'll make one final table here now and changed the visualizations accordingly. This should be the final result! Of course this explains the memory usage of Hungarian.jl ;)
| Matrix size | Lib seconds | Lib memory | Own seconds | Own memory |
|---|---|---|---|---|
| 800 | 0.18 | 0.18MiB | 0.46 | 95MiB |
| 1000 | 0.26 | 0.2MiB | 0.74 | 117MiB |
| 2000 | 0.62 | 0.3MiB | 1.29 | 124Mib |
| 4000 | 1.5 | 0.7MiB | 3.0 | 153MiB |
| 8000 | 4.0 | 1.4MiB | 5.6 | 155MiB |
| 16000 | 11.7 | 3.5MiB | 12.2 | 197MiB |
| 20000 | 17.3 | 3.8MiB | 16.2 | 191MiB |
| 30000 | 35.1 | 5.5MiB | 24.7 | 197MiB |
| 40000 | 60.1 | 6.2MiB | 36.5 | 191MiB |
Okay and a short plot for memory and speed:
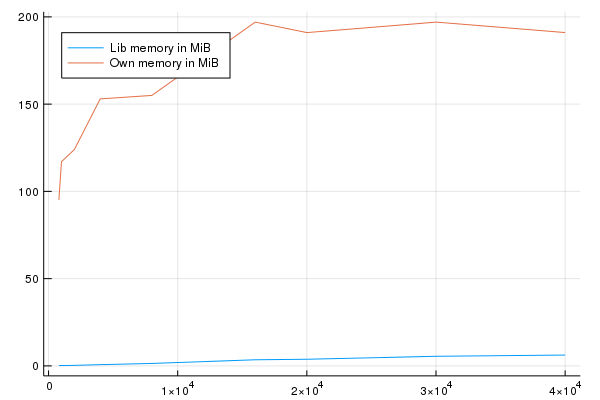
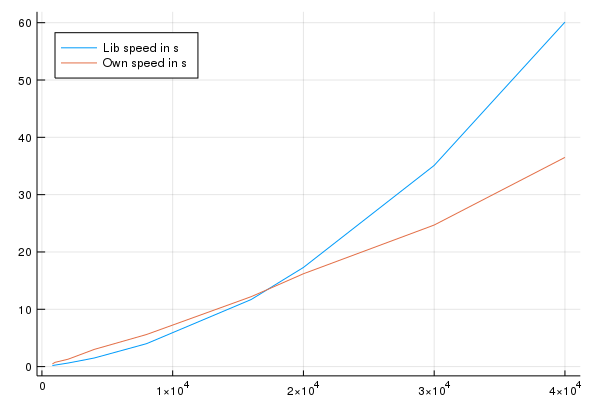
This shows that the memory usage of my algorithm both algorithms seems to be linear is not rising very quickly with a relatively high starting point on my side which I will check in a second. The duration is also not growing as fast as the one from the library. You can see that for large arrays \(> 20,000 \times 20,000\) my algorithm is faster.
Okay I don't really get why the starting point of memory is so high maybe some of you know additional improvements.
I hope you learned something in this blog post ;)
Checkout my code in the GitHub repository.
I'll keep you updated if there are any news on this on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de
Thanks for reading!
If you enjoy the blog in general please consider a donation via Patreon. You can read my posts earlier than everyone else and keep this blog running.
Reading this post and hopefully the one about the Hungarian method I assume you might be interested in:
The Simplex method series about linear programming
Want to be updated? Consider subscribing on Patreon for free


