Solving the Megaron-Cube with Python
Creation date: 2016-09-19
The Megaron-Cube is a puzzle where six different blocks should be combined to form a 3x3x3 cube. I tried to solve it a couple of times but never get it. It's cheating to use a program, I know...
... well it can be seen as another challenge and maybe I am better at this one.
What is the Megaron-Cube?
The Megaron-Cube has the following six blocks which must be combined to build a 3x3x3 cube.
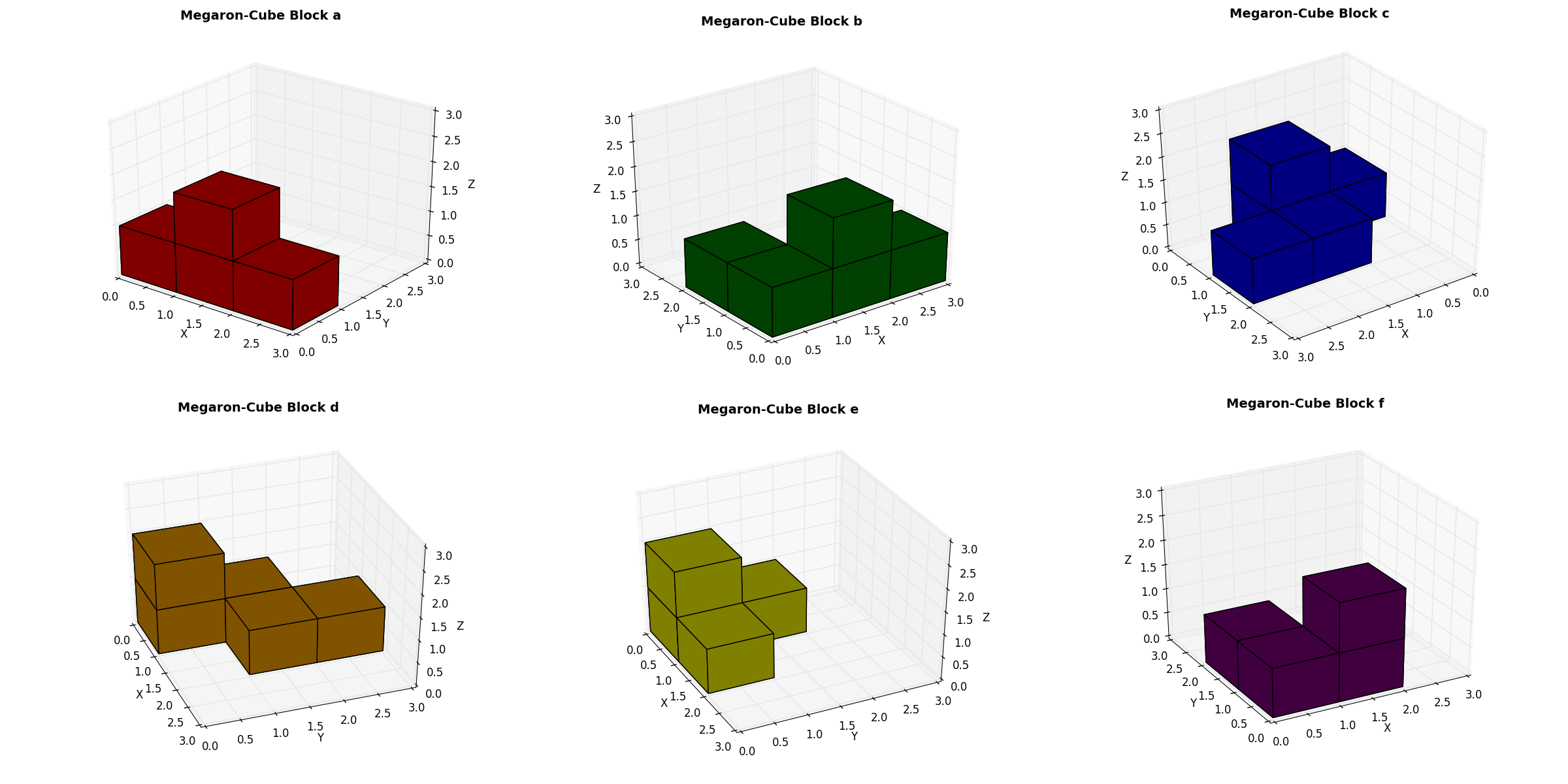
As shown the six blocks are all different. For our visualization we will use these different colors. Normally the blocks are made of wood.
How to draw these blocks with Python?
I don't want to solve this puzzle without visualizing the solution. It is easier to check whether the solving steps are correct if they can be visualized.
First of all these packages are needed:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from itertools import product, combinations
import math3d as m3d
import mathYou probably need to install math3d using pip install math3d. It is used to rotate our blocks.
We will start with drawing a single cube at a defined position in the 3x3x3 grid. Therefore a 3d matplotlib figure is defined.
fig = plt.figure()
fig.suptitle('Megaron-Cube', fontsize=14, fontweight='bold')
ax = fig.gca(projection='3d')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')To draw a single cube we will use
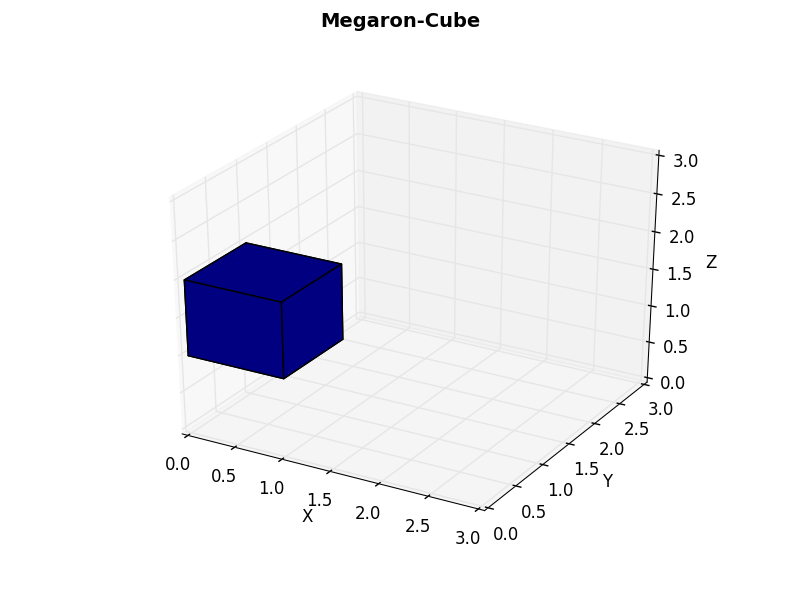
drawCube(ax,0,0,1,"blue")
ax.set_xlim3d(0, 3)
ax.set_ylim3d(0, 3)
ax.set_zlim3d(0, 3)
plt.show()Here we call the drawCube function. A blue cube should be drawn at position [0,0,1]. The set_ rows define that we see the whole 3x3x3 grid. Now the drawCube function must be defined.
def drawCube(ax,x,y,z,color):
r = [0,1]
X, Y = np.meshgrid(r, r)
ax.plot_surface(x+X,y+Y,z+1, alpha=1, color=color) # top
ax.plot_surface(x+X,y+Y,z+0, alpha=1, color=color) # bottom
ax.plot_surface(x+X,y+0,z+Y, alpha=1, color=color) # front
ax.plot_surface(x+X,y+1,z+Y, alpha=1, color=color) # back
ax.plot_surface(x+0,y+X,z+Y, alpha=1, color=color) # left
ax.plot_surface(x+1,y+X,z+Y, alpha=1, color=color) # rightThe meshgrid function returns coordinate matrices X and Y for the coordinate vector [0,1]. Output:
X:
[[0 1]
[0 1]]
Y:
[[0 0]
[1 1]]A single surface for our cube can be drawn using the plot_surface function. This function needs those coordinate matrices or a single value (here z+1).
ax.plot_surface(x+X,y+Y,z+1, alpha=1, color=color) # topThe whole cube for our function call drawCube(ax,0,0,1,"blue") will look like this:
Let's define our six blocks by setting the position of those cubes. In this step we define the colors of the blocks as well.
color = {}
color["a"] = "red"
color["b"] = "green"
color["c"] = "blue"
color["d"] = "orange"
color["e"] = "yellow"
color["f"] = "purple"
"""
define all blocks
"""
blocks = {}
blocks["a"] = np.array([[0,0,0],[1,0,0],[2,0,0],[1,0,1]])
blocks["b"] = np.array([[0,0,0],[1,0,0],[2,0,0],[1,0,1],[0,1,0]])
blocks["c"] = np.array([[0,0,0],[1,0,0],[1,0,1],[1,1,0],[2,1,0]])
blocks["d"] = np.array([[0,0,0],[0,0,1],[0,1,0],[1,1,0],[1,2,0]])
blocks["e"] = np.array([[0,0,0],[1,0,0],[0,1,0],[0,0,1]])
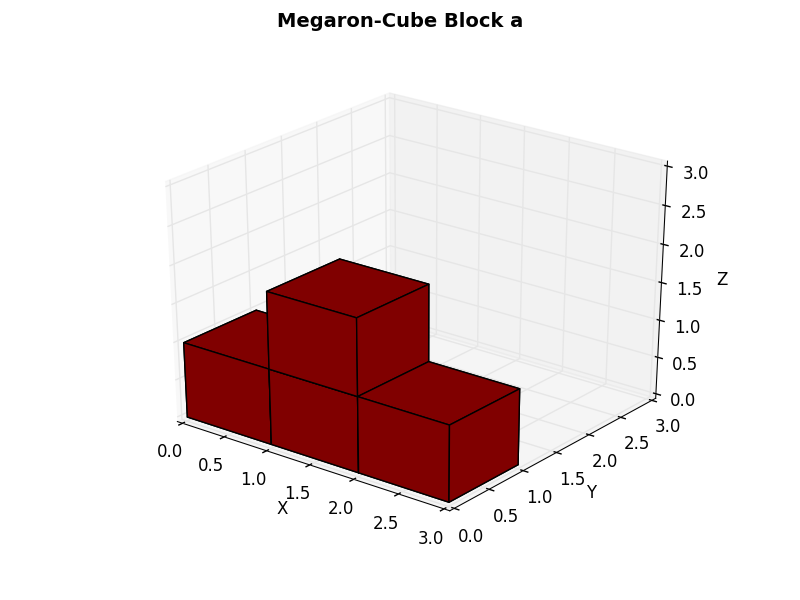
blocks["f"] = np.array([[0,0,0],[1,0,0],[0,1,0],[1,0,1]])The first block has cubes in four positions [[0,0,0],[1,0,0],[2,0,0],[1,0,1]].
We want to draw the blocks in the same order therefore we define a list:
list_blocks = ["a","b","c","d","e","f"]The aim is to draw every single block at every possible position. These two lines give us all positions inside the 3x3x3 cube.
r3 = range(3)
poss = list(product(r3,r3,r3))To get all rotations the following rotation vectors are used:
deg = 90
rad = deg*math.pi/180
rz = m3d.Orientation.new_axis_angle([0,0,1], rad)
ry = m3d.Orientation.new_axis_angle([0,1,0], rad)
rx = m3d.Orientation.new_axis_angle([1,0,0], rad)As the naming shows rz defines the rotation about the z-axis.
To get all rotations we use a cartesian product again.
protations = [False,rz,ry,rx]
protations = list(product(protations,protations,protations,protations))False means that we don't rotate. A list of some protations (possible rotations), where some of them might result in the same object.
[(False, False, False, False),
(False, rx, ry, False),
(ry, ry, ry, False), ... ]The last row describes a combination of three rotations about the y-axis. Each False value will be ignored therefore (False, rx, ry, False) is the same as (rx, False, ry, False).
These protations array must be transformed in a rotation object.
rotations = [False]
for r in protations:
cr = m3d.Orientation.new_axis_angle([1,0,0], 0)
for t in r:
if t is not False:
cr *= t
if cr not in rotations:
rotations.append(cr)Here a rotations array is initialized where the first rotation (no rotation) is stored. For all tuples in protations the single rotations are combined using cr *= t if t is not False. The current rotation cr is first defined as a rotation about the x-axis with a 0 rad angle (no rotation). At the end of this block we check if the rotation is already part of rotations to remove duplicates like the one mentioned above.
The goal is to show all possible block positions for each block.
for cblock in list_blocks:
for rotation in rotations:
for pos in poss:
boolCheck, cubes = checkCubes(cblock,blocks[cblock],pos,rotation)
if boolCheck:
ax.clear()
drawCubes(ax,cubes,color[cblock])
ax.set_xlim3d(0, 3)
ax.set_ylim3d(0, 3)
ax.set_zlim3d(0, 3)
plt.pause(0.5)
while True:
plt.pause(50)For each defined block in list_blocks we iterate over all rotations and positions. Then we check whether the cubes are reasonable. Here reasonable means that the block is inside the 3x3x3 grid and that it wasn't drawn before. Otherwise some blocks would be drawn several times because they are symmetrical. If the cube is reasonable we will draw it and pause for 0.5 seconds before the next reasonable block is drawn. At the end we pause to show the last block until...
Let's have a look at the simple drawCubes function first.
def drawCubes(ax,cubes,color):
for cube in cubes:
drawCube(ax,cube[0],cube[1],cube[2],color)Each block is defined as a list of cubes which can be drawn as single cubes.
Now we will check if a block is reasonable. The parameters name, block, pos and rot are used. name defines a name for the current block which is one of a-f. The block is the list of cubes for the block. pos defines the position of the first cube in the block and rot is the rotation parameter.
def checkCubes(name,block,pos,rot):
global obj_pos
global obj_fields
cubes = []
for cube in block:
cube = getCube(cube,pos,rot)
cubes.append(cube)
for val in cube:
if val < 0 or val > 2:
return False, cubes
cubes.sort()
if cubes in obj_pos[name]:
return False, cubes
obj_pos[name].append(cubes)
field = np.zeros((3,3,3))
for cube in cubes:
field[cube] += 1
obj_fields[name].append(field)
return True, cubesThis function uses two global variables which are defined at the top of the program:
from collections import defaultdict
obj_pos = defaultdict(list)
obj_fields = defaultdict(list)They are used to check whether a block is drawn already.
All cubes for the blocks are computed and it is check if one of those cube points is outside of the 3x3x3 cube.
cubes = []
for cube in block:
cube = getCube(cube,pos,rot)
cubes.append(cube)
for val in cube:
if val < 0 or val > 2:
return False, cubesIt uses the getCube function which rotates a cube and translate it.
def getCube(cube,pos,rot):
if rot is not False:
cube_vec = m3d.Vector(*cube)
cube = list(rot*cube_vec)
cube = [ int(round(x)) for x in cube ]
return tuple([x + y for x, y in zip(cube, pos)])Afterwards the cubes list is sorted. This array:
[(0, 0, 0), (1, 0, 0), (2, 0, 0), (1, 0, 1)]is sorted to:
[(0, 0, 0), (1, 0, 0), (1, 0, 1), (2, 0, 0)]This defines the same block. Rotations which get the same block again like a rotation about 360 degrees have the same sorted representation. This is used in the following rows.
cubes.sort()
if cubes in obj_pos[name]:
return False, cubes
obj_pos[name].append(cubes)The positions are saved to check if the block is already drawn and to draw the cubes faster for the following steps. Then a representation of the 3x3x3 cube (field) is saved where only the current block is mapped.
field = np.zeros((3,3,3))
for cube in cubes:
field[cube] = 1
obj_fields[name].append(field)
return True, cubesThe representation for

is mapped to:
[[[ 1. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
[[ 1. 1. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
[[ 1. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]]Using this functions we are able to draw every possible position of every block. The next step is to combine those blocks. It is an essential speed up to save all possible positions for each blocks which is done in checkCubes. Therefore we call these function for all blocks,positions and rotations.
for cblock in list_blocks:
for rotation in rotations:
for pos in poss:
checkCubes(cblock,blocks[cblock],pos,rotation)Now we can get the number of possible positions for each block.
pos_lengths = [range(len(obj_pos[x])) for x in list_blocks]
print(pos_lengths)Not the length itself is saved but the range which makes things easier in future steps.
Let's get all combinations for the first two blocks.
possibleCombinations = list(product(pos_lengths[0],pos_lengths[1]))These possibleCombinations might not be really possible but don't know how to call them ;)
The idea of the next part of our programm is to get all real possibilities of two blocks. If a combination is possible we will add the next block to it until all six blocks are possible. Then we found a solution.
We will add possibilities so we use a while loop which is stopped if there is no possible combination left which should be checked.
p = 0
while p < len(possibleCombinations):Then we check if the current position of blocks is possible:
combination = possibleCombinations[p]
checkBool = checkListOfCubes(combination)checkBool is True if the current combination is really possible and False otherwise. The combination tuple looks something like (1,4) or (1,4,8). The first integer defines the position of block "a" the second the position of block "b" and so on.
Blocks aren't able to combine if a position is used more than once. We define an empty field which represents the 3x3x3 cube and add the blocks defined in combination. If a position is used more than once False is returned and True otherwise.
def checkListOfCubes(combination):
global list_blocks
global obj_fields
field = np.zeros((3,3,3))
for p_idx in range(len(combination)):
p = combination[p_idx]
field += obj_fields[list_blocks[p_idx]][p]
if np.max(field) > 1:
return False
return TrueLet's go back into our while loop:
p = 0
while p < len(possibleCombinations):
combination = possibleCombinations[p]
checkBool = checkListOfCubes(combination)Now we want to add the next block if the current combination is possible.
if checkBool:
block_no = len(combination)
if block_no < len(list_blocks):
for q in pos_lengths[block_no]:
lcombination = list(combination)
lcombination.append(q)
possibleCombinations.append(tuple(lcombination))
if len(combination) == len(list_blocks):
solutions.append(combination)block_no defines the next block no which we want to add if it exists. Then we add all positions that are possible for this new block to the list of possibleCombinations. If we used all six blocks we found a solution and append it to solutions.
After the while loop we save the solutions and the positions of the blocks using pickle.
save_obj("solutions",solutions)
save_obj("obj_pos",obj_pos)The function is defined as:
def save_obj(filename, obj):
with open(filename+'.pickle', 'wb') as handle:
pickle.dump(obj, handle)Visualization of the Solution
Let's visualize the solution in a different programm called drawSolution.py. It uses some variables and functions which are described earlier.
First of all we load the solutions and the positions of the blocks.
def load_obj(filename):
with open(filename+'.pickle', 'rb') as handle:
return pickle.load(handle)
solutions = load_obj("solutions")
obj_pos = load_obj("obj_pos")Now we can draw the solutions:
for combination in solutions:
ax.clear()
list_of_cubes = []
list_of_colors = []
for block_idx in range(len(combination)):
block = list_blocks[block_idx]
cubes = obj_pos[block][combination[block_idx]]
list_of_cubes.append(cubes)
list_of_colors.append(color[block])
for cube_idx in range(len(list_of_cubes)):
cubes = list_of_cubes[cube_idx]
c = list_of_colors[cube_idx]
drawCubes(ax,cubes,c)
ax.set_xlim3d(0, 3)
ax.set_ylim3d(0, 3)
ax.set_zlim3d(0, 3)
plt.pause(5)First all blocks are added to list_of_cubes and the colors to list_of_colors. Afterwards they are drawn using drawCubes.

Okay but how many solutions are there and how fast can we solve it?
There are 24 solutions and it takes about a minute to find them.
If you tried to solve this puzzle you might think... Wow 24 solutions and I didn't find at least one of them? Calm down :) It's not that bad. There is only a single real solution and the other ones are mirrored.
Improvements
If we are able to remove those mirrored solutions it will be faster because less combinations must be checked. To remove them the first block can be used to reduce the search space.
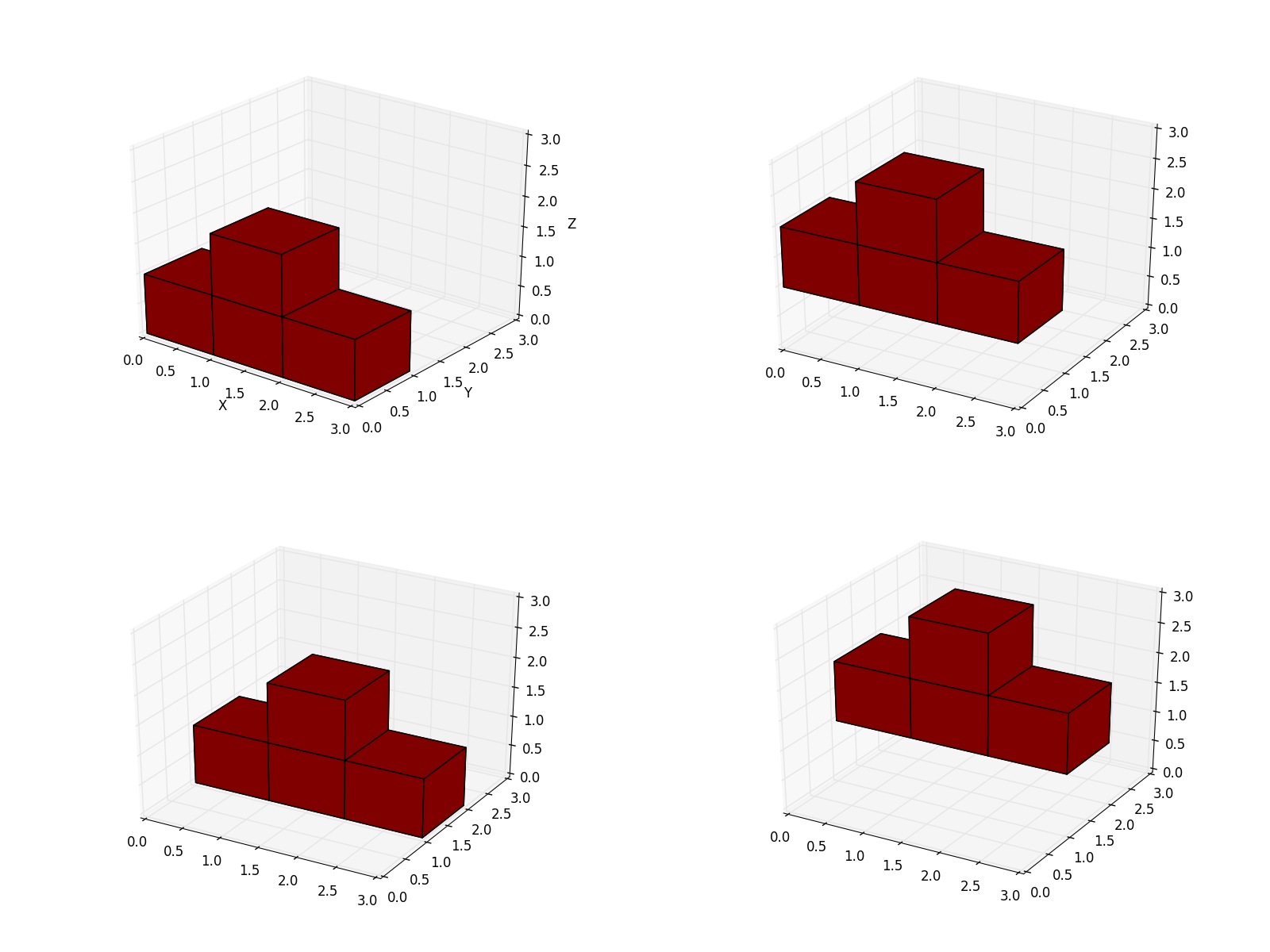
At the moment there are 72 possible positions for the first block.
Let's have a look at a few of them.
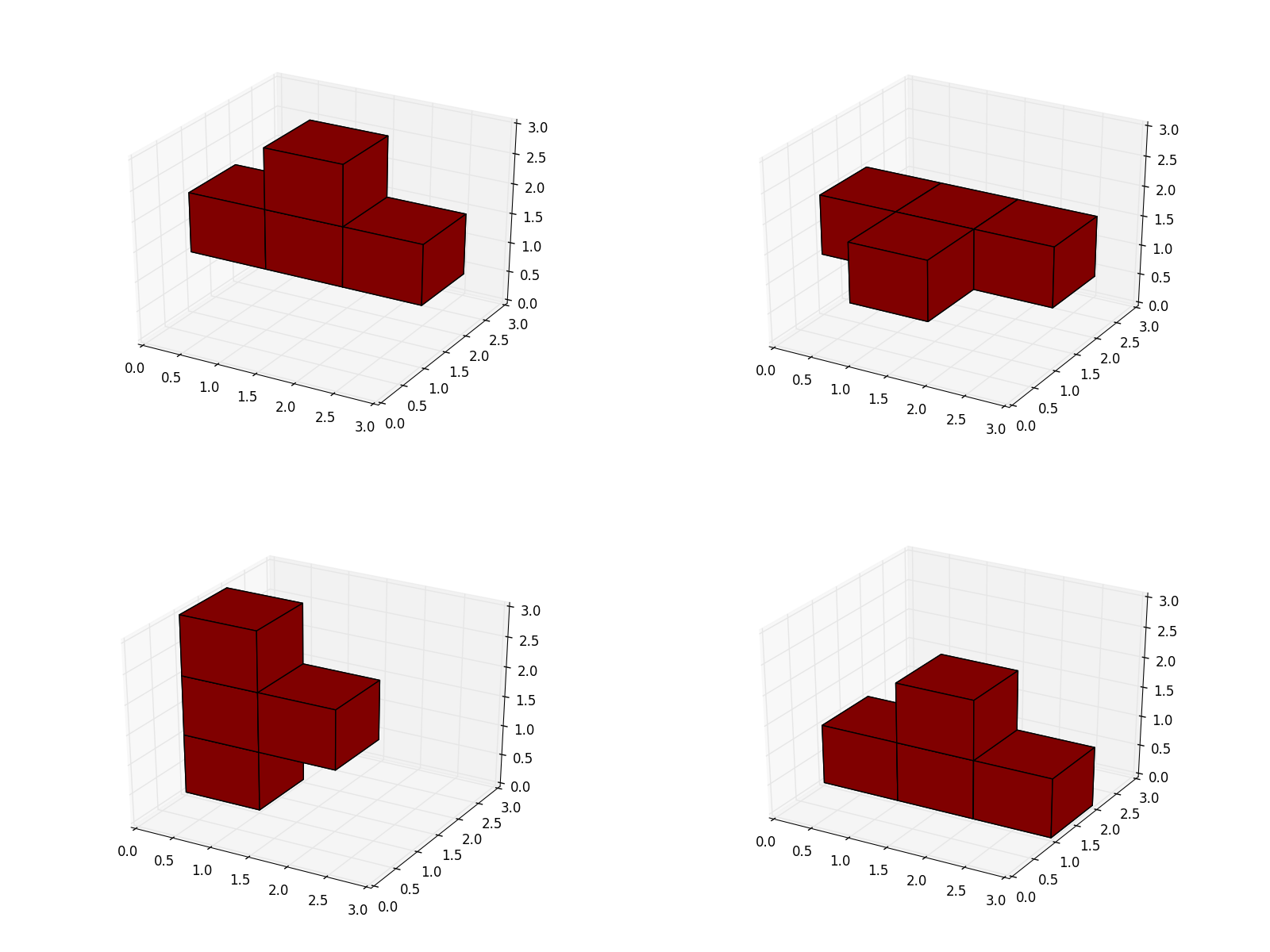
The first two images are the same if we rotate the 3x3x3 cube. Same is true for the other two visualizations.
All in all are there only four real positions for the first block.
We used the following to get all positions for each block.
for cblock in list_blocks:
for rotation in rotations:
for pos in poss:
checkCubes(cblock,blocks[cblock],pos,rotation)Now we want only those four positions of the first block so this is used instead:
cblock = list_blocks[0]
for pos in poss:
if pos[1] != 2:
checkCubes(cblock,blocks[cblock],pos,False)
for cblock in list_blocks[1:]:
for rotation in rotations:
for pos in poss:
checkCubes(cblock,blocks[cblock],pos,rotation)It takes only 2.5 seconds on my machine to solve it now and a single solution is generated.
At least one further improvement is possible. Some combinations of blocks are possible but it can be seen that they can't be part of the overall solution like the following one:

It is not reasonable because there is a single block (bottom right) which can't be filled. Each block has at least four cubes. Therefore we can remove all combinations where the smallest hole is smaller than four.
This check will be done in checkListOfCubes at the end instead of return True.
return checkZeroNeighborField(field)The idea is to check how big the biggest block can be that fills an empty cube.
We need several functions to get this representation. First of all we get all neighbors for each position and save them in a global object.
neighborsObj = {}
def getNeighborsPos(pos):
global neighborsObj
neighbors = []
for t in [[0,0,1],[0,1,0],[1,0,0],[0,0,-1],[0,-1,0],[-1,0,0]]:
test = [pos[0]+t[0],pos[1] + t[1],pos[2]+t[2]]
if max(test) <= 2 and min(test) >= 0:
neighbors.append(test)
neighborsObj[pos] = neighbors
return neighborsEach cube has at most six possible neighbors. At least one of them is not inside the 3x3x3 cube if pos is not the middle position (1,1,1).
They are saved in the neighborsObj somewhere at the beginning of our program using:
for pos in poss:
getNeighborsPos(pos)We are interested in all empty positions in our field so only the empty neighbors are relevant.
def getZeroNeighbors(field,pos):
neighbors = neighborsObj[tuple(pos)]
zero_neighbors = []
for neighbor in neighbors:
if field[neighbor[0],neighbor[1],neighbor[2]] == 0:
zero_neighbors.append(neighbor)
return zero_neighborsThe next step is to get the longest path using only the empty neighbors from a defined position. This path is computed with the following function:
def getLongestZeroPath(field, pos):
path = []
pathObj = {}
neighbors2check = getZeroNeighbors(field,pos)
for neighbor in neighbors2check:
path.append(neighbor)
pathObj[tuple(neighbor)] = 1
c = 0
while len(neighbors2check) > 0:
c+=1
neighbor = neighbors2check.pop(0)
for n in getZeroNeighbors(field,neighbor):
if tuple(n) not in pathObj:
path.append(n)
pathObj[tuple(n)] = 1
neighbors2check.append(n)
return pathWe define the path using an array and a faster object to check if the position is already inside the path. Firstly all direct neighbors are added to the path.
Then for each of those neighbors the empty neighbors which are not part of the path are added and so on.
For the last step to get the representation of biggest blocks for each position the following function is used.
def checkZeroNeighborField(field):
r3 = range(3)
neighborsMap = np.zeros((3,3,3))
for pos in product(r3,r3,r3):
if field[pos[0],pos[1],pos[2]] == 0:
if neighborsMap[pos[0],pos[1],pos[2]] == 0:
zeroPath = getLongestZeroPath(field,pos)
len_zeroPath = len(zeroPath)
if len_zeroPath < 4:
return False
neighborsMap[pos[0],pos[1],pos[2]] = len_zeroPath
for point in zeroPath:
neighborsMap[point[0],point[1],point[2]] = len_zeroPath
else:
neighborsMap[pos[0],pos[1],pos[2]] = -1
return TrueFor each position we check if it is an empty position. If not empty we set the value in our neighborsMap to -1. Otherwise we compute the longest zero path and return False if the path is shorter than four because our smallest blocks have four cubes. It is not needed to compute the getLongestZeroPath for each position. The function is only reasonable if the current position is not part of a path before.
This improvement solves the puzzle in about 0.6 seconds. Which is one hundredth of our first run-time.
Hope you enjoyed this different kind of blog post.
If you enjoy the blog in general please consider a donation via Patreon. You can read my posts earlier than everyone else and keep this blog running.
Interested in more?
You can download all the code on my OpenSourcES GitHub repo.
Want to be updated? Consider subscribing on Patreon for free


