Random Forest Regression from scratch used on Kaggle competition

Creation date: 2019-05-01

I normally write some code and some days, weeks, month later when everything is done I write a blog about it. I think the blog is more structured that way but maybe it has less details and my errors in between aren't that visible anymore (just if someone of you comment afterwards ;) ) Thanks for that. It really helps improve my code and this blog. In the past couple of weeks I wanted to understand random forest better and not just how to use them so I've built my own package. For me it's not satisfying enough to use a machine learning package and tune the parameters I really like to build stuff from scratch. That's basically the reason for this blog I see too many blogs about: "How to use random forest?", "How to achieve an awesome accuracy for MNIST?" but as mentioned in my post about the latter there aren't many who dive deeper into it and actually use it for real (well and blog about it).

I learn a lot doing this and also when I blog about it and especially when I learn through comments but it also takes quite some time to write these posts. If you've read multiple of my posts and learned a good amount please consider a donation via Patreon to keep it going. Thank you very much!

Of course for everyone else I keep to continue writing and you can't pay everyone on the internet just because you read a post from them. It's more about whether you enjoy this blog for a longer time now and found something you didn't elsewhere.

Back to the track. I'm using random forest for my current Kaggle Challenge about predicting earth quakes. I might publish an extra article about that one when it's done but for now I want to use my Random Forest package on a different challenge which is more for fun (I mean I do the other for fun as well but Kaggle/LANL are paying money for the winners) whereas this one is purely for training. It's about predicting house prices based on some features.

This post is on different aspects

Creating a julia package (basics)
Explaining random forest
Simple features first
What can be improved?

I've only have my random forest code at the moment so my score in the competition might (and probably will) turn out quite bad. Anyway the goal in general is to learn random forest (by coding it) and somehow apply it.

Creating a julia package

First let's create our RandomForestRegression package. Starting julia in your favorite projects folder.

(v1.1) pkg> generate RandomForestRegression

That creates a folder RandomForestRegression with:

src/
    - RandomForestRegression.jl
Project.toml

and the RandomForestRegression.jl looks like this:

module RandomForestRegression

greet() = print("Hello World!")

end # module

we later want to add some dependencies to it but for now we are done. Normally you should also add a test folder etc... Probably you want to have a look at the official documentation: Creating a julia package.

Explaining Random Forest

Maybe you're here and have never heard of random forest: Random forests can be used to classify data based on features or for doing regression. They basically work on building several simple models and combining them together so the principle is the crowd is wiser than a single model. It's called a forest because the crowd is formed of so called decision trees. Additionally it is called random as decision trees are created in a random manner. You might think: Okay if we have 10 stupid models and combine them together we have a single stupid model but it actually is quite effective. Let's have a look at my favorite example of that:

In there Hannah Fry talks about a study where pigeons diagnose breast cancer and they do that with an astonishing accuracy which gets even better when the pigeons are combined to a super pigeon.

This is basically what random forests are about. Now we have to understand decision trees first and for that I use the simple question whether I want to play Frisbee next Wednesday. It depends on the weather and whether I'm in Heidelberg. I split the weather part into temperature and precipitation. The Heidelberg question is a simple yes or no one. I might have the following previous knowledge:

Temperature	Precipitation	In Town	Frisbee
20	0	1	1
25	15	0	0
8	80	1	0
10	68	1	1

and can ask simple logic questions about one feature at a time. What is the probability that I participate if the temperature is below 15 degrees? According to the table the answer is 50% which is not that useful. The question: What is the chance that I play Frisbee if the temperature is below 10 degrees would be more useful as there isn't a case where I played Frisbee when it was colder than 10 degrees. A question like this can be represented as node in the tree with two children. A complete tree might look like this:

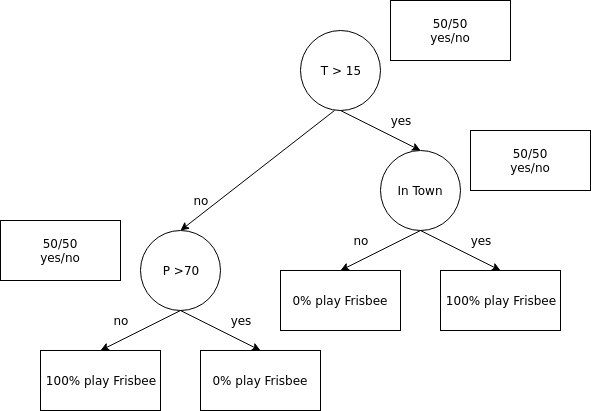
Now there might be a new data point with a temperature of 10 degrees and a precipitation of less than 70 but I'm not in Heidelberg. Therefore I wouldn't play Frisbee but the decision tree would be sure that I do. Nevertheless it contains probably some amount of truth that I enjoy playing more when the weather isn't too bad. Additionally it would probably be a good idea to have a look at the current wind speed as well but let's return back to random forests.

What we are going to do is to create several of those decision trees in a random way and later combine the results.

The example above is a classification task whereas I will code random forest for regression but it's basically the same. I'll explain the differences later on.

In general there are a few key points for random forest and the most important one I would say is the question of where to split if a feature is already selected. As explained above the temperature can be split into $\leq 15$ and $> 15$ or into $\leq 9$ and $>9$ both are valid but the second one gives more information. We didn't gain knowledge with the first (we just split it into two parts) but with the second one we changed the chances from 50/50 to 0/100 and 66/33.

You can read more about information gain in this post (medium.com)

I'll explain the gain later for regression tasks.

Let's dive into code ;)

What do we need:

A representation for a decision tree
- a node
Combined to a forest

The node needs:

Which feature was used
Where was the split (like >15 or >9)
Which entries are still present in this node
Information about children
Information about the current result

For the third point I mean in the frisbee example we only have row 1 and row 2 left on the right branch after the split on temperature. The current result for regression is basically the answer to: If this is the leaf node what do we predict and I take the mean here.

For example if we have the housing prices ranging from 10,000€ to 5,000,000€ with a mean of 130,000€ we first use 130,000€ for every new entry as we don't have any better guess now. What to use can depend on the loss function but the mean is the simplest. Now we know that the city has a single garage and there are no places for less than 50,000€ with that property but the really expensive ones have more than one garage so the price is bounded above by 400,000€ and the mean didn't change. If we instead ask does it have a garage in general we don't have the upper bound and the mean rises.

Btw I'm using € instead of $ because it gets confused with the Latex environment and I always have to write <span>$</span> otherwise :D

In the above example we continued our tree until we reached the end and the "mean" or class was determined perfectly but this doesn't have to be the case.

This is the current data structure:

mutable struct Node
    feature    :: Int64 
    comp_value :: Float64
    data_idxs  :: Vector{Int64}
    mean       :: Float64
    left_child :: Union{Nothing, Node}
    right_child:: Union{Nothing, Node}
    
    Node() = new()
end

mutable struct Tree
    root                :: Node
    Tree() = new()
end

and then the structure for creating a tree is roughly this:

function create_random_forest(feature_matrix, train_ys, ntrees)
    forest = Vector{Tree}()
    tc = 1
    total_nfeatures = size(feature_matrix)[1]
    nfeatures_per_tree = 5
    ncols_per_tree = convert(Int64,floor(length(train_ys)/2))

    while tc < ntrees
        feature_idx = sample(1:total_nfeatures, nfeatures_per_tree; replace=false)
        cols = sample(1:length(train_ys), ncols_per_tree; replace=false)

        tree = create_random_tree(feature_matrix, feature_idx, cols, train_ys, total_nfeatures)
        if tree.root.left_child != nothing
            push!(forest,tree)
            tc += 1
        else
            println("Couldn't create tree!!")
        end
        flush(stdout)
    end
    return forest
end

We want to create a certain number of trees and in each tree we only have a look at x features and only part of the data.

Btw I have the features as rows here and the data entries per column as selecting from an array in Julia is faster by column and I access that more often.

The if statement is to check whether there was at least a split in the root node sometimes the feature is so bad that all the data points considered for that tree have the same value then we don't want to add it to the forest.

For some of the parts I would like to have only a pseudo code style as it is just a big amount of code partly because I optimized it for parallel execution.

For creating a tree we have:

function create_random_tree(glob_feature_matrix, ...)

tree = Tree() 
@views feature_matrix = glob_feature_matrix[feature_idx, cols]
root, queue = create_root_node!(...)

while length(queue) > 0
    node = popfirst!(queue)
    left_node, right_node = compute_node!(...)
    if left_node != nothing
        queue_compute_nodes!(...)
    end
end
tree.root = root
return tree
end

Here we create a view of the data we will actually use for our tree first. Without @views this would create a copy. Then we create the first node (the root node) and put the children in a queue we have to process. Take one from the queue, process and put back in the queue if there are children.

First I created a recursive version out of it as it helps me for tree like structures but is actually wasteful as you have to deal with recursion depth so it's always a good idea to reformulate it into a queue.

The next important part is to find a good split value. I'm doing it as follows:

get a random feature
create 200 splitting points between min and max value
compute the sum of the standard deviation of both children
select the split point with the minimal sum

Sometimes there is no split which means there would be only one child. Then the split isn't doing anything and we check for a different random feature up to a point where we just don't want anymore and say there is nothing we can do and simply say it's a leaf node now.

For example there might be three houses which all have 2 bedrooms, 1 bathroom and no garage and in the current tree we only have #bedrooms, #bathrooms and #garages as our features but they have the prices 100,000€ 75,000€ and 130,000€ because they are in different regions for example. Three is nothing more we can do in this tree so we take the mean value and proceed with other open nodes in the tree or create a new tree.

There are some things I learned especially during this stage which might be partly obvious:

Don't compute features every time you use it.
The standard deviation (if corrected) of a single element is NaN.

Regarding the first one: I did this because I wanted to be for flexible and have somehow a random computation in between but this takes way too much time and isn't generalizable enough.

and the second one:

\[ s=\sqrt{\frac{1}{N-1} \sum_{i=1}^{N}\left(x_{i}-\overline{x}\right)^{2}} \]

that is the sample standard deviation which divides by the number of samples -1 and this is the one I thought of:

\[ s=\sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\overline{x}\right)^{2}} \]

in that one you divide by N so if you have one sample you get the value - its mean which is 0. In the first you get 0/0 which is NaN.

Numpy is using the second one by default and you can use the parameter ddof to get the first. Julia on the other hand or more precisely the Statistics package is using the first which really confused me as this obviously broke my code as I trying to minimize the sum and 0 is very good at minimizing a non negative number and NaN is the worst you can get. (Yes it's worse than Infinity)

Actually I'm not too sure which of these above is the better one to use in general so I took the standard approach in Julia but wrapped it in my own function which just returns 0 if it's one element. I think I should use the first as I do sampling in the broad range but maybe someone can comment on that who uses this more frequently than I do ;)

Regarding the Statistics package. Whenever you create a package which uses other packages (has dependencies) you have to use:

>cd /your/package
>julia
julia> ]
(v1.1) pkg> activate .  
(RandomForestRegression) pkg> add Statistics

This will change or create your Project.toml and your Manifest.toml file.

The other thing we have to do is to actually run the prediction.

For every tree:
- Begin in the root node and traverse done following the decisions
- Until you get to a leaf node and return the mean value saved there

In the end combine the mean values. I think that is pretty basic. I do some additional things here and there but let's try to use it for our House pricing challenge for now and for the rest I'll create a different post if you want. Here are some things I tried

Parallelize the code
Remove some predictions if you think they aren't good
Trying to get a feeling of which features are the best

Go download the Kaggle data!

For now I've selected only the simple numeric features:

using DataFrames, CSV

file = "./data/train.csv"
df = CSV.File(file) |> DataFrame!

feature_cols = [:LotFrontage, :LotArea, :OverallQual, :OverallCond, :YearBuilt, :TotalBsmtSF, Symbol("1stFlrSF"), 
                Symbol("2ndFlrSF"), :BedroomAbvGr, :KitchenAbvGr, :TotRmsAbvGrd, :GarageCars]

pred_col = :SalePrice

println(df[1:10,vcat(feature_cols,pred_col)])

which gives this as an output:

julia> include("housing.jl")
10×13 DataFrame
│ Row │ LotFrontage │ LotArea │ OverallQual │ OverallCond │ YearBuilt │ TotalBsmtSF │ 1stFlrSF │ 2ndFlrSF │ BedroomAbvGr │ KitchenAbvGr │ TotRmsAbvGrd │ GarageCars │ SalePrice │
│     │ String      │ Int64   │ Int64       │ Int64       │ Int64     │ Int64       │ Int64    │ Int64    │ Int64        │ Int64        │ Int64        │ Int64      │ Int64     │
├─────┼─────────────┼─────────┼─────────────┼─────────────┼───────────┼─────────────┼──────────┼──────────┼──────────────┼──────────────┼──────────────┼────────────┼───────────┤
│ 1   │ 65          │ 8450    │ 7           │ 5           │ 2003      │ 856         │ 856      │ 854      │ 3            │ 1            │ 8            │ 2          │ 208500    │
│ 2   │ 80          │ 9600    │ 6           │ 8           │ 1976      │ 1262        │ 1262     │ 0        │ 3            │ 1            │ 6            │ 2          │ 181500    │
│ 3   │ 68          │ 11250   │ 7           │ 5           │ 2001      │ 920         │ 920      │ 866      │ 3            │ 1            │ 6            │ 2          │ 223500    │
│ 4   │ 60          │ 9550    │ 7           │ 5           │ 1915      │ 756         │ 961      │ 756      │ 3            │ 1            │ 7            │ 3          │ 140000    │
│ 5   │ 84          │ 14260   │ 8           │ 5           │ 2000      │ 1145        │ 1145     │ 1053     │ 4            │ 1            │ 9            │ 3          │ 250000    │
│ 6   │ 85          │ 14115   │ 5           │ 5           │ 1993      │ 796         │ 796      │ 566      │ 1            │ 1            │ 5            │ 2          │ 143000    │
│ 7   │ 75          │ 10084   │ 8           │ 5           │ 2004      │ 1686        │ 1694     │ 0        │ 3            │ 1            │ 7            │ 2          │ 307000    │
│ 8   │ NA          │ 10382   │ 7           │ 6           │ 1973      │ 1107        │ 1107     │ 983      │ 3            │ 1            │ 7            │ 2          │ 200000    │
│ 9   │ 51          │ 6120    │ 7           │ 5           │ 1931      │ 952         │ 1022     │ 752      │ 2            │ 2            │ 8            │ 2          │ 129900    │
│ 10  │ 50          │ 7420    │ 5           │ 6           │ 1939      │ 991         │ 1077     │ 0        │ 2            │ 2            │ 5            │ 1          │ 118000    │

Okay I wanted to select only the simple numeric ones which didn't work out as we have a NA in the first column. I'll set that to 0 for now. I know that is not the best way to handle this.

Changed it to:

df = df[:,vcat(feature_cols,pred_col)]

function isNotValid(x, type)
    try 
        nx = parse(type, x)
        return false
    catch
        return true
    end
end
df[isNotValid.(df[:,1], Int64),1] = "0"
df[:,1] = parse.(Int64, df[:,1])

println(df[1:10,:])

Now we have to create our feature matrix. Remember that it is a transposed version of the current representation:

df = disallowmissing!(df)
feature_matrix = transpose(convert(Matrix, df[:,feature_cols]))

for transpose we have to add using LinearAlgebra.

Let's add our RandomForestRegression package and try it out: Before we do that we have to add our package not only with using RandomForestRegression but we also need to include it to our julia environment with ] dev . if we are in the root directory.

For a basic test let's run this:

train_ys = convert(Vector{Float64}, df[:,pred_col])

forest = RFR.create_random_forest(feature_matrix, train_ys, 20)

pred_ys = RFR.predict_forest(forest, feature_matrix; default=mean(train_ys))

mae = sum(abs.(pred_ys.-train_ys))/length(pred_ys)
println("MAE: ", mae)
println("RMSLE: ", rmsd(log.(pred_ys), log.(train_ys)))

println("")
println("What if we just take the mean?")
pred_ys = mean(train_ys)*ones(length(train_ys))
mae = sum(abs.(pred_ys.-train_ys))/length(pred_ys)
println("MAE: ", mae)
println("RMSLE: ", rmsd(log.(pred_ys), log.(train_ys)))

This gives us:

MAE: 15981.995280550193
RMSLE: 0.1282110792581262

What if we just take the mean?
MAE: 57434.77027584912
RMSLE: 0.407600507698506

RMSLE (Root mean squared logarithmic error) is the evaluation metric for this challenge on Kaggle.

We shouldn't run the prediction on the same points as we trained so let's split it into the first 80% for training and the rest as cross validation:

nof_real_train = convert(Int64, floor(0.8*length(train_ys)))
println("Train on ",nof_real_train, " of ", length(train_ys))
real_train_ys = train_ys[1:nof_real_train]
@views train_feature_matrix = feature_matrix[:,1:nof_real_train]
cv_ys = train_ys[nof_real_train+1:end]
@views cv_feature_matrix = feature_matrix[:,nof_real_train+1:end]

forest = RFR.create_random_forest(train_feature_matrix, real_train_ys, 20)

pred_ys = RFR.predict_forest(forest, cv_feature_matrix; default=mean(real_train_ys))

with this result:

MAE: 24592.147691338712
RMSD: 0.18937660129611758

What if we just take the mean?
MAE: 56982.804325389385
RMSD: 0.39754831118733847

Let's do this for the test data and submit our results and call it done for now ;)

test_file = "./data/test.csv"
test_df = CSV.File(test_file) |> DataFrame!

test_df = test_df[:,vcat(:Id,feature_cols)]
check_valid_cols = [:LotFrontage,:GarageCars,:TotalBsmtSF]
for col in check_valid_cols
    test_df[isNotValid.(test_df[:,col], Int64),col] = "0"
    test_df[:,col] = parse.(Int64, test_df[:,col])
end

test_df = disallowmissing!(test_df)

test_feature_matrix = convert(Array, transpose(convert(Matrix, test_df[:,feature_cols])))

pred_test_ys = RFR.predict_forest(forest, test_feature_matrix; default=mean(real_train_ys))

submission_df = DataFrame(Id=test_df[:Id], SalePrice=pred_test_ys)
CSV.write("data/submission_basic.csv", submission_df)

This takes me to rank 3635/4488 with a score of 0.18956 which is pretty much the same as our cv score.

I hoped for a better score but well I used only a handful of features didn't combine them and it was just a simple test overall.

Anyway I hoped you learned something and maybe you want to use the code as it is for now for your own project or this one and do some more advanced feature engineering or improve my code. ;)

Checkout the code in the GitHub repository.

Additionally as I'm building things from scratch... there is obviously already a Random Forests package written in Julia. Let's give that one a try:

using DecisionTree

# julia package
feature_matrix = convert(Matrix, df[:,feature_cols])
nof_real_train = convert(Int64, floor(0.8*length(train_ys)))
println("Train on ",nof_real_train, " of ", length(train_ys))
real_train_ys = train_ys[1:nof_real_train]
train_feature_matrix = feature_matrix[1:nof_real_train,:]
cv_ys = train_ys[nof_real_train+1:end]
cv_feature_matrix = feature_matrix[nof_real_train+1:end,:]

model = build_forest(real_train_ys, train_feature_matrix, 8, 100)
pred_ys = apply_forest(model, cv_feature_matrix)

mae = sum(abs.(pred_ys.-cv_ys))/length(pred_ys)
println("With the RandomForests julia package: ")
println("MAE: ", mae)
println("RMSD: ", rmsd(log.(pred_ys), log.(cv_ys)))

test_feature_matrix = convert(Array, convert(Matrix, test_df[:,feature_cols]))

pred_test_ys = apply_forest(model, test_feature_matrix)

submission_df = DataFrame(Id=test_df[:Id], SalePrice=pred_test_ys)
CSV.write("data/submission_julia_pkg.csv", submission_df)

I've submitted it to Kaggle and got a score of 0.16 which is better than from my package ;)

I hope I was able to explain you the basics of random forest and how to implement it in general.

I'll keep you updated if there are any news on this on Twitter OpenSourcES as well as my more personal one: Twitter Wikunia_de

Thanks for reading!

If you enjoy the blog in general please consider a donation via Patreon. You can read my posts earlier than everyone else and keep this blog running.

Want to be updated? Consider subscribing on Patreon for free

Subscribe to RSS

OpenSourc.ES

Random Forest Regression from scratch used on Kaggle competition

Creating a julia package

Explaining Random Forest